题目内容
10．已知函数f（x）=ax（a＞0且a≠1）的图象经过点（2，$\frac{1}{9}$）．（1）比较f（2）与f（b2+2）的大小；
（2）求函数g（x）=a${\;}^{{x}^{2}-2x}$（x≥0）的值域．
分析 （1）求出a的值，根据函数的单调性比较函数值的大小即可；（2）根据函数的单调性求出函数的值域即可．
解答 解：（1）由已知得：a2=$\frac{1}{9}$，解得：a=$\frac{1}{3}$，
∵f（x）=${（\frac{1}{3}）}^{x}$在R递减，则2≤b2+2，
∴f（2）≥f（b2+2）；
（2）∵x≥0，∴x2-2x≥-1，
∴${（\frac{1}{3}）}^{{x}^{2}-2x}$≤3，
故g（x）的值域是（0，3]．
点评 本题考查了函数的单调性、最值问题，考查指数函数的性质，是一道基础题．
练习册系列答案
相关题目
20．设p：x＜3，q：-1＜x＜2，则p是q成立的（ ）
| A． | 充分必要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
如图，建立平面直角坐标系xoy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．
5．
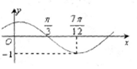函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到g（x）=sinωx的图象，则只要将f（x）的图象（ ）
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到g（x）=sinωx的图象，则只要将f（x）的图象（ ）| A． | 向左平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{3}$个单位长度 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度 | D． | 向左平移$\frac{π}{6}$个单位长度 |
7．已知命题p：?x∈R，sinx＞1，则（ ）
| A． | ?p：?x∈R，sinx≤1 | B． | ?p：?x∈R，sinx≤1 | C． | ?p：?x∈R，sinx≤1 | D． | ?p：?x∈R，sinx＞1 |