题目内容
17.已知函数f(x)=ex-e-x.(Ⅰ)判断函数f(x)的奇偶性和单调性,并说明理由;
(Ⅱ)若f(x2)+f(kx+1)>0对任意x∈R恒成立,求k的取值范围.
分析 (Ⅰ)根据题意,对于函数f(x)=ex-e-x,先分析其定义域,在求出f(-x),分析f(x)与f(-x)的关系,即可得函数f(x)为奇函数,由函数f(x)的解析式,对其求导可得f′(x)=ex+e-x,分析导数的符号,即可得函数f(x)的单调性;
(Ⅱ)结合函数的奇偶性和单调性分析可得:f(x2)+f(kx+1)>0对任意x∈R恒成立等价于x2+kx+1>0对任意x∈R恒成立,由二次函数的性质分析可得答案.
解答 解:(Ⅰ)根据题意,函数f(x)=ex-e-x,
其定义域为R,关于原点对称,f(-x)=e-x-ex=-(ex-e-x)=-f(x),故函数f(x)为奇函数,
其导数f′(x)=ex+e-x>0,则函数f(x)为增函数,
(Ⅱ)由(Ⅰ)可得:函数f(x)为奇函数且在R上为增函数,
f(x2)+f(kx+1)>0⇒f(x2)>-f(kx+1)⇒f(x2)>f(-kx-1)⇒x2>(-kx-1)⇒x2+kx+1>0,
即x2+kx+1>0对任意x∈R恒成立,
则有k2-4<0,
解可得-2<k<2;
故k的取值范围是(-2,2).
点评 本题考查函数奇偶性与单调性的综合应用,关键是分析得到函数f(x)的奇偶性与单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知各项均为正数的等比数列{an}中,如果a2=1,那么这个数列前3项的和S3的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | [2,+∞) | D. | [3,+∞) |
9.设a=log38,b=21.2,c=0.33.1,则( )
| A. | b<a<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
12.与-123°终边相同的角k是(k∈Z)( )
| A. | 123° | B. | 237°+360°k | C. | 123°+180°k | D. | 270°+180°k |
13.在矩形ABCD中,AB=4,AD=3,若向该矩形内随机投一点P,那么使得△ABP与△ADP的面积都不小于2的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{7}$ | D. | $\frac{4}{9}$ |
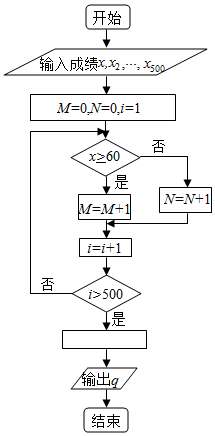 如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.
如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.