题目内容
函数f（x）=（ex+e-x）sinx的部分图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：通过函数的奇偶性，排除部分选项，然后利用0＜x＜π时的函数值，判断即可．
解答：
解：函数f（-x）=（e-x+ex）（-sinx）=-（ex+e-x）sinx=-f（x），
∴函数f（x）=（ex+e-x）sinx是奇函数，排除B、D；
当0＜x＜π时，f（x）＞0，排除C．
∴A满足题意．
故选：A．
∴函数f（x）=（ex+e-x）sinx是奇函数，排除B、D；
当0＜x＜π时，f（x）＞0，排除C．
∴A满足题意．
故选：A．
点评：本题考查函数的图象的判断，一般通过函数的定义域、值域．单调性，奇偶性，变化趋势等知识解答．
练习册系列答案
阅读快车系列答案
相关题目
将函数y=2sinx图象上所有点向右平移
个单位，然后把所得图象上所有点的横坐标变为原来的
倍（纵坐标不变），得到y=f（x）的图象，则下列对f（x）描述正确的是（ ）
| π |
| 6 |
| 1 |
| 2 |
A、f（x）的对称轴是x=
| ||||
| B、f（x）的周期是4π | ||||
C、f（x）分单调增区间是[4kπ-
| ||||
D、一个对称中心是（
|
命题p：
≤0；命题q：y=xa（x为自变量）在第一象限是增函数，则p是q的（ ）
| a |
| a-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
直线3x-4y+12=0与圆x2+y2+10x-6y-2=0的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、相交且过圆心 |
某校高二年级文科共303名学生，为了调查情况，学校决定随机抽取50人参加抽测，采取先简单随机抽样去掉3人然后系统抽样抽取出50人的方式进行．则在此抽样方式下，某学生甲被抽中的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
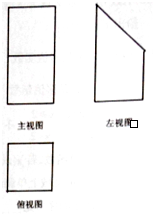某几何体的三视图如图所示，俯视图是边长为1的正方形，主视图上下都是边长为1的正方形，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
| D、2 |