题目内容

已知直线l1：ax+3y+1=0，l2：x+（a-2）y+a=0．若l1∥l2，则直线l1与l2之间的距离为（　　）
A、
2
3
B、
2
2
3
C、
4
3
D、
4
2
3
考点：两条平行直线间的距离
专题：计算题,直线与圆
分析：由平行可得a=3，进而可得直线方程，代入距离公式可得答案．
解答： 解：当l1∥l2时，有
a(a-2)-3=0
3a-(a-2)≠0
，解得a=3，
此时，l1，l2的方程分别为：3x+3y+1=0，x+y+3=0即3x+3y+9=0，
故它们之间的距离为d=
4
2
3
．
故选：D．
点评：本题考查直线的一般式方程的平行关系，涉及平行线间的距离公式，属基础题．
练习册系列答案
相关题目
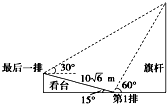某校运动会开幕式上举行升旗仪式，在坡度为15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10
6
 m（如图），则旗杆的高度为（　　）
A、10 m
B、30 m
C、10
3
 m
D、10
6
 m
若0＜x＜y＜1，则（　　）
A、3y＜3x
B、(
1
4
)x＜(
1
4
)y
C、logx3＜logy3
D、x-
3
2
＞y-
3
2
已知抛物线x2=y+1上一定点A（-1，0）和两动点P、Q，当PA⊥PQ时，点Q的横坐标的取值范围（　　）
A、（-∞，-3]∪[1，+∞）
B、[1，+∞）
C、[-3，-1]
D、（-∞，-3]
在抛物线y2=4x上恒有两点关于直线l：y=kx+3则对称，k的取值范围是（　　）
A、-1＜k＜0
B、0＜k＜1
C、-1≤k≤0
D、0≤k≤1
sin
7π
6
的值为（　　）
A、
1
2
B、
3
2
C、-
1
2
D、-
3
2
设变量x、y满足约束条件
2x-y≤2
x-y≥-1
x+y≥1
，则z=2x+3y的最大值为（　　）
A、18B、2C、3D、0
复数Z=
2
-i3
1-
2
i
，则复数
.
Z
对应的点在（　　）
A、第一象限或第三象限
B、y轴负半轴上
C、x轴正半轴上
D、第二象限或第四象限
在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρsin（θ-
π
4
）=3
2
，曲线C2的直角坐标方程为
x2
16
+
y2
9
=1．
（Ⅰ）求曲线C1的直角坐标方程；
（Ⅱ）已知P为曲线C2上一点，Q为曲线C1上一点，求P、Q两点间距离的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网