题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、等腰三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、直角三角形 |
考点:三角形的形状判断
专题:解三角形
分析:利用正弦定理可得sinAcosC>sinB,再利用两角和的正弦计算可得cosA<0,从而可得答案.
解答:
解:△ABC中,∵cosC>
,
∴由正弦定理得:cosC>
,又sinA>0,
∴sinAcosC>sinB=sin(A+C)=sinAcosC+cosAsinC,
∴cosAsinC<0,又sinC>0,
∴cosA<0,A为钝角,
故选:C.
| b |
| a |
∴由正弦定理得:cosC>
| sinB |
| sinA |
∴sinAcosC>sinB=sin(A+C)=sinAcosC+cosAsinC,
∴cosAsinC<0,又sinC>0,
∴cosA<0,A为钝角,
故选:C.
点评:本题考查三角形的形状的判断,考查正弦定理与两角和的正弦的应用,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设5x+1=a,5y-1=b,则5x+y=( )
| A、a+b | ||
| B、ab | ||
| C、a-b | ||
D、
|
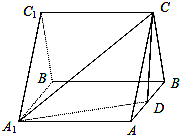 如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.
如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点. 设函数f(x)=|x+2|+|x-1|
设函数f(x)=|x+2|+|x-1|