题目内容
设实部为正数的复数z,满足|z|=
,且复数(1+2i)z在复平面上对应的点在第一、三象限的角平分线上.
(1)求复数z;
(2)若
+
(m∈R)为纯虚数,求实数m的值.
| 10 |
(1)求复数z;
(2)若
. |
| z |
| m-i |
| 1+i |
考点:复数代数形式的混合运算,复数求模
专题:数系的扩充和复数
分析:(1)设Z=a+bi(a,b∈R且a>0),由条件可得a2+b2=10①,a=-3b②.由①②联立的方程组得a、b的值,即可得到z的值.
(2)根据若
+
(m∈R)为纯虚数,可得
,由此求得m的值.
(2)根据若
. |
| z |
| m-i |
| 1+i |
|
解答:
解:(1)设Z=a+bi(a,b∈R且a>0),由|Z|=
得:a2+b2=10①.
又复数(1+2i)z=(a-2b)+(2a+b)i在复平面上对应的点在第一、三象限的角平分线上,
则a-2b=2a+b,即a=-3b②.
由①②联立的方程组得a=3,b=-1;或a=-3,b=1.
∵a>0,∴a=3,b=-1,则Z=3-i.
(2)∵
+
=3+i+
=
+
i 为纯虚数,∴
,
解得m=-5.
| 10 |
又复数(1+2i)z=(a-2b)+(2a+b)i在复平面上对应的点在第一、三象限的角平分线上,
则a-2b=2a+b,即a=-3b②.
由①②联立的方程组得a=3,b=-1;或a=-3,b=1.
∵a>0,∴a=3,b=-1,则Z=3-i.
(2)∵
. |
| Z |
| m-i |
| 1+i |
| (m-i)(1-i) |
| 2 |
| m+5 |
| 2 |
| 1-m |
| 2 |
|
解得m=-5.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
 已知函数f(x)=Acos(ωx+φ)的图象如图所示(A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ)的图象如图所示(A>0,ω>0,|φ|<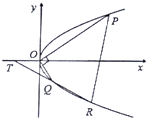 如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q
如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q