题目内容
已知函数f(x)=sinx-ax-bxcosx(a∈R,b∈R).
(1)若b=0,讨论函数f(x)在区(0,π)上的单调性;
(2)若a=2b且a≥
,对任意的x>0,试比较f(x)与0的大小.
(1)若b=0,讨论函数f(x)在区(0,π)上的单调性;
(2)若a=2b且a≥
| 2 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)问中,分a≥1,a≤-1,-1<a<1进行讨论;
(2)中引进新函数g(x),将问题转化为求新函数的单调性问题.
(2)中引进新函数g(x),将问题转化为求新函数的单调性问题.
解答:
解:(1)b=0时,f(x)=sinx-ax,则f′(x)=cosx-a,
当a≥1时,f′(x)<0,所以函数f(x)在区间(0,π)上单调递减;
当a≤-1时,f′(x)>0,所以函数f(x)在区间(0,π)上单调递增;
当-1<a<1时,存在θ∈(0,π),使得cosθ=a,即f(θ)=0,
①x∈(0,θ)时,f′(x)>0,函数f(x)在区间(0,θ)上单调递增,
②x∈(θ,π)时,f′(x)<0,函数f(x)在区间(θ,π)上单调递减.
(2)a=2b时,f(x)=sinx-
x(2+cosx),猜测f(x)<0恒成立,
证明:f(x)<0等价于
<
x,
令g(x)=
-
x,
则g(x)=
-
=-3(
-
)2-
+
,
当
≥
,即a≥
时,g′(x)≤0,g(x)在区间(0,+∞)上单调递减,
所以当x>0时,g(x)<g(0)=0,即f(x)<0恒成立.
当a≥1时,f′(x)<0,所以函数f(x)在区间(0,π)上单调递减;
当a≤-1时,f′(x)>0,所以函数f(x)在区间(0,π)上单调递增;
当-1<a<1时,存在θ∈(0,π),使得cosθ=a,即f(θ)=0,
①x∈(0,θ)时,f′(x)>0,函数f(x)在区间(0,θ)上单调递增,
②x∈(θ,π)时,f′(x)<0,函数f(x)在区间(θ,π)上单调递减.
(2)a=2b时,f(x)=sinx-
| a |
| 2 |
证明:f(x)<0等价于
| sinx |
| 2+cosx |
| a |
| 2 |
令g(x)=
| sinx |
| 2+cosx |
| a |
| 2 |
则g(x)=
| 2cosx+1 |
| (2+cosx)2 |
| a |
| 2 |
| 1 |
| 2+cosx |
| 1 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
当
| a |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
所以当x>0时,g(x)<g(0)=0,即f(x)<0恒成立.
点评:本题属于利用导数求函数的单调性问题,解题过程中用到了分类讨论思想,转化思想.

练习册系列答案
相关题目
已知函数 f(x)=ax3+f′(2)x2+3,若 f′(1)=-5,则f′(2)=( )
| A、-l | B、-2 | C、-3 | D、-4 |
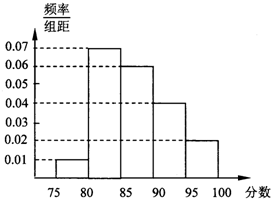 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: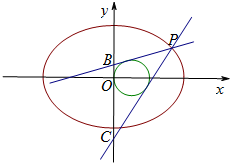 设椭圆E:
设椭圆E: