题目内容
 如图,在山脚A测得山顶P的仰角为30°,沿倾斜角为15°的斜坡向上走a米到B,在B处测得山顶P的仰角为60°,求山高h=( )
如图,在山脚A测得山顶P的仰角为30°,沿倾斜角为15°的斜坡向上走a米到B,在B处测得山顶P的仰角为60°,求山高h=( )A、
| ||||
B、
| ||||
C、
| ||||
| D、a |
考点:解三角形的实际应用
专题:综合题,解三角形
分析:设α=30°,β=15°,△PAB中,∠PAB=α-β=15°,∠BPA=(
-α)-(
-γ)=γ-α=30°,由正弦定理可求PB,根据PQ=PC+CQ=PB•sinγ+asinβ 可得结果.
| π |
| 2 |
| π |
| 2 |
解答:
解:设α=30°,β=15°
△PAB中,∠PAB=α-β=15°,∠BPA=(
-α)-(
-γ)=γ-α=30°,
∴
=
,∴PB=
a.
∴PQ=PC+CQ=PB•sinγ+asinβ=
a×sin60°+asin15°=
a米.
故选:A.
△PAB中,∠PAB=α-β=15°,∠BPA=(
| π |
| 2 |
| π |
| 2 |
∴
| a |
| sin30° |
| PB |
| sin15° |
| ||||
| 2 |
∴PQ=PC+CQ=PB•sinγ+asinβ=
| ||||
| 2 |
| ||
| 2 |
故选:A.
点评:本题考查正弦定理的应用,直角三角形中的边角关系,求出PB是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知函数 f(x)=ax3+f′(2)x2+3,若 f′(1)=-5,则f′(2)=( )
| A、-l | B、-2 | C、-3 | D、-4 |
在复平面内,复数
对应的点位于( )
| -3+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图是甲,乙两名同学5次综合测评成绩的茎叶图,下列四个结论中,正确的是( )
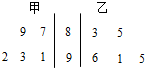

| A、甲成绩的极差大于乙成绩的极差 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的平均值等于乙成绩的平均值 |
| D、甲成绩的标准差小于乙成绩的标准差 |

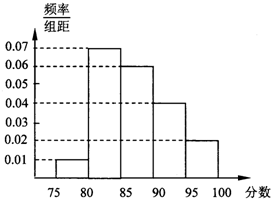 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: