题目内容
3．函数y=e|lnx|的图象大致为（ ）| A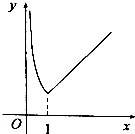． |  | B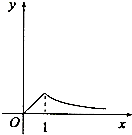． |  | C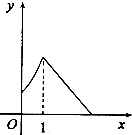． |  | D． |  |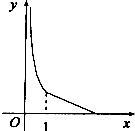
分析 根据复合函数的单调性即可判断．
解答 解：因为t=|lnx|=$\left\{\begin{array}{l}{ln\frac{1}{x}，0＜x＜1}\\{lnx，x≥1}\end{array}\right.$，
当0＜x＜1时，函数y=|lnx|为减函数，
当x≤1时，函数y=|lnx|为增函数，
又因为y=ex为增函数，
所以y=e|lnx|在（0，1）上为减函数，在[1，+∞）为增函数，
故选：A．
点评 本题考查了复合函数的单调性以及绝对值函数的图象和性质，属于基础题．
练习册系列答案
相关题目
11．
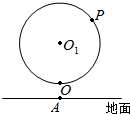如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A．风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为（ ）
如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A．风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为（ ）| A． | 5 | B． | 4$+\sqrt{7}$ | C． | 4$+\sqrt{17}$ | D． | 4$+\sqrt{19}$ |
15．已知函数$f（x）=\left\{\begin{array}{l}x+2，x≤0\\ 1gx，x＞0\end{array}\right.$，则函数y=|f（x）|-1的零点个数是（ ）
| A． | 1 | B． | 4 | C． | 3 | D． | 2 |
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，CA=CB=CC1=1，则直线A1B与平面BB1C1C所成角的正弦值为$\frac{\sqrt{3}}{3}$．
13．某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据制成频率分布表如下
（1）求频率分布表中x的值；
（2）如果上学路上所需时间不少于60分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿；
（3）现有5名上学路上时间小于40分钟的新生，其中3人上学路上时间不小于20分钟，则从这5人中任选2人，设这2人中上学路上时间小于20分钟人数为X，求X的分布列和数学期望．
（1）求频率分布表中x的值；
（2）如果上学路上所需时间不少于60分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿；
（3）现有5名上学路上时间小于40分钟的新生，其中3人上学路上时间不小于20分钟，则从这5人中任选2人，设这2人中上学路上时间小于20分钟人数为X，求X的分布列和数学期望．
| 分组 | 频率 |
| [0，20） | 0.25 |
| [20，40） | x |
| [40，60） | 0.13 |
| [60，80） | 0.06 |
| [80，100） | 0.06 |