题目内容
已知椭圆C的两个焦点为F1(-3,0),F2(3,0),点M是椭圆C上的动点,且MF1?MF2的最大值为25.
(1)求椭圆C的方程;
(2)已知有一定点N(2,0),求MN的最小值.
(1)求椭圆C的方程;
(2)已知有一定点N(2,0),求MN的最小值.
考点:椭圆的简单性质,椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)由椭圆的定义可知,MF1+MF2=2a,再由基本不等式求出MF1•MF2的最大值a2,再由a,b,c的关系,即可得到方程;
(2)令M(5cosα,4sinα),运用两点间的距离公式,化简三角函数,并配方结合余弦函数的值域,即可切得最小值.
(2)令M(5cosα,4sinα),运用两点间的距离公式,化简三角函数,并配方结合余弦函数的值域,即可切得最小值.
解答:
解:(1)设椭圆方程为
+
=1(a>b>0),
则c=3,MF1+MF2=2a,MF1•MF2≤(
)2=a2,
当且仅当MF1=MF2,取最大值a2,
则a2=25,b2=a2-c2=16.
则椭圆C的方程
+
=1.
(2)令M(5cosα,4sinα),由于N(2,0),
MN=
=
=
,
由于
∉[-1,1],
则cosα=1时,MN取最小值3.
| x2 |
| a2 |
| y2 |
| b2 |
则c=3,MF1+MF2=2a,MF1•MF2≤(
| MF1+MF2 |
| 2 |
当且仅当MF1=MF2,取最大值a2,
则a2=25,b2=a2-c2=16.
则椭圆C的方程
| x2 |
| 25 |
| y2 |
| 16 |
(2)令M(5cosα,4sinα),由于N(2,0),
MN=
| (5cosα-2)2+16sin2α |
| 9cos2α-20cosα+20 |
=
9(cosα-
|
由于
| 10 |
| 9 |
则cosα=1时,MN取最小值3.
点评:本题考查椭圆的标准方程和定义,以及参数方程的运用,考查基本不等式的运用和三角函数的最值求法,属于中档题.

练习册系列答案
相关题目
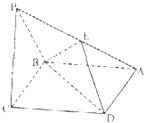 己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.
己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.