题目内容
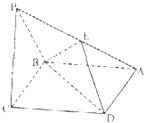 己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.
己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.(Ⅰ)求证:平面EBD⊥平面ABCD:
(Ⅱ)求三棱锥VP-BED的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明面面垂直一般利用面面垂直的判定定理故可连接EO可利用中位线定理证得EO∥PC再结合PC⊥平面ABCD可得EO⊥平面ABCD即可得证.
(Ⅱ)利用等体积转换,即可求三棱锥VP-BED的体积.
(Ⅱ)利用等体积转换,即可求三棱锥VP-BED的体积.
解答:
(Ⅰ)证明:连结AC交BD于点O,连结OE,则O是AC的中点.
又知E是AP中点
∴EO∥PC,
∵PC⊥平面ABCD,∴OE⊥平面ABCD.
又知OE?平面BDE,
∴平面EBD⊥平面ABCD
(Ⅱ)解:VP-BED=VD-BEP=
VP-BEA=
a3.
又知E是AP中点
∴EO∥PC,
∵PC⊥平面ABCD,∴OE⊥平面ABCD.
又知OE?平面BDE,
∴平面EBD⊥平面ABCD
(Ⅱ)解:VP-BED=VD-BEP=
| 1 |
| 2 |
| ||
| 12 |
点评:本题主要考查了利用面面垂直的判定定理证明面面垂直,考查体积的计算,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
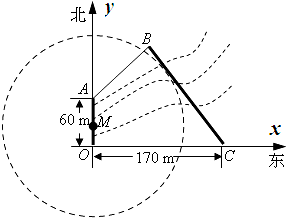 如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.
如图:为了保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸).规划要求:新桥BC与河岸AB垂直,保护区的边界为圆心M(在线段OA上)与BC相切的圆.建立如图所示的直角坐标系,已知新桥BC所在直线的方程为:4x+3y-680=0.