题目内容
15.已知圆锥的底面半径为r,其轴截面为直角三角形,则该圆锥的侧面积为$\sqrt{2}πr$2.分析 根据轴截面的特点求出母线长,代入侧面积公式即可.
解答 解:设圆锥母线为l,∵圆锥轴截面为直角三角形,∴2l2=4r2,解得l=$\sqrt{2}r$.
∴圆锥的侧面积S=πrl=$\sqrt{2}π{r}^{2}$.
故答案为:$\sqrt{2}π{r}^{2}$.
点评 本题考查了圆锥的结构特征和侧面积计算,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
7.已知数列{an}与{bn}满足bn+1-bn=3(an+1-an),n∈N*,在数列{an}中,an=$\frac{{n}^{2}}{3}$-16n,设数列{bn}中的最小项是第k项,则k等于( )
| A. | 30 | B. | 28 | C. | 26 | D. | 24 |
4.某种型号的书包原价为a元,如果连续两次以相同的百分率x降价,那么两次降价后价格为多少元?( )
| A. | a(1-x) | B. | a(1-x)2 | C. | a(1-2x) | D. | 以上都不是 |




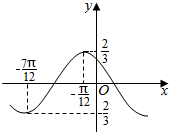 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示