题目内容
20.求函数y=x-$\sqrt{1-x}$的值域.分析 由题意可得函数y=x-$\sqrt{1-x}$为(-∞,1]上的增函数,代值计算可得值域.
解答 解:由1-x≥0可解得x≤1,故函数的定义域为(-∞,1],
又可得函数y=x-$\sqrt{1-x}$为(-∞,1]上的增函数,
∴当x=1时,函数取最大值1,
故函数的值域为(-∞,1].
点评 本题考查函数的值域,得出函数的定义域和单调性是解决问题的关键,属基础题.

练习册系列答案
相关题目
16.如图,点(x,y)在阴影部分所表示的平面区域上,则z=y-x的最大值为( )
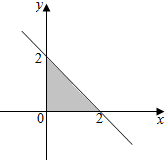

| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
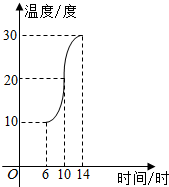 如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.