题目内容
设
=(2,1),
=(sinθ,cosθ),其中θ∈(0,
)为过点A(1,4)的直线l的倾斜角,若当
•
最大时,直线l恰好与圆(x+1)2+(y-2)2=r2(r>0)相切,则r= .
| m |
| n |
| π |
| 2 |
| m |
| n |
考点:数量积的坐标表达式,圆的切线方程
专题:平面向量及应用,直线与圆
分析:根据向量数量积公式和辅助角公式的出当
•
最大时θ的值,从而得到直线l的方程,再由圆心到直线的距离等于半径列式运算即可.
| m |
| n |
解答:
解:∵
=(2,1),
=(sinθ,cosθ),
∴
•
=2sinθ+cosθ
=
sin(θ+μ),其中tanμ=
.
∵θ∈(0,
)
∴当θ+μ=
时,
•
=2sinθ+cosθ有最大值.
此时tanμ=
,
即直线l的斜率为2
∴直线l的方程为y-4=2(x-1)
即,2x-y+2=0.
∵圆(x+1)2+(y-2)2=r2(r>0)的圆心为(-1,2)
∴圆心到直线的距离d=
=
,
∴r=
.
| m |
| n |
∴
| m |
| n |
=
| 5 |
| 1 |
| 2 |
∵θ∈(0,
| π |
| 2 |
∴当θ+μ=
| π |
| 2 |
| m |
| n |
此时tanμ=
| 1 |
| 2 |
即直线l的斜率为2
∴直线l的方程为y-4=2(x-1)
即,2x-y+2=0.
∵圆(x+1)2+(y-2)2=r2(r>0)的圆心为(-1,2)
∴圆心到直线的距离d=
| |-2-2+2| | ||
|
2
| ||
| 5 |
∴r=
2
| ||
| 5 |
点评:本题主要考查了向量的数量积的坐标运算,三角恒等变换直线与圆的位置关系等知识的综合应用,以及转化与化归的思想方法,属于难题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
(理科)已知满足条件x2+y2≤1的点(x,y)构成的平面区域的面积为S1,满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域的面积为S2,(其中[x]、[y]分别表示不大于x、y的最大整数),则下列关系正确的是( )
| A、S1=S2 |
| B、S1>S2 |
| C、S1<S2 |
| D、S22+S12=π2 |
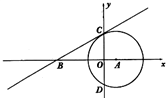 已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为