题目内容
12.在棱长为1的正方体AC1中,E,F,M,N分别为棱AB,CD,DD1,CC1的中点,点P在四边形AEFD内及其边界上运动,点Q在四边形MNC1D1内及其边界上运动,则线段PQ的中点G的轨迹所形成的几何体的体积为( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{32}$ | D. | $\frac{3}{32}$ |
分析 建立空间坐标系,设P,Q的坐标,求出G的坐标的范围,得出G的轨迹,求出体积.
解答  解:以D为原点建立空间坐标系如图,
解:以D为原点建立空间坐标系如图,
设P(x,y,0),Q(a,0,c).则G($\frac{x+a}{2}$,$\frac{y}{2}$,$\frac{c}{2}$).
∵点P在四边形AEFD内及其边界上运动,点Q在四边形MNC1D1内及其边界上运动,
∴0$≤x≤\frac{1}{2}$,0≤y≤1,0≤a≤1,$\frac{1}{2}≤c≤1$.
∴0≤$\frac{x+a}{2}$≤$\frac{3}{4}$,0≤$\frac{y}{2}$≤$\frac{1}{2}$,$\frac{1}{4}$≤$\frac{c}{2}$≤$\frac{1}{2}$.
∴G点轨迹形成的几何体是边长分别为$\frac{3}{4}$,$\frac{1}{2}$,$\frac{1}{4}$的长方体.
∴V=$\frac{3}{4}$×$\frac{1}{2}$×$\frac{1}{4}$=$\frac{3}{32}$.
故选:D.
点评 本题考查了空间几何体的判断,体积计算,结合坐标范围判断几何体的形状是关键.

练习册系列答案
相关题目
3.函数y=sin($\frac{1}{2}$x+θ)是偶函数,则θ的一个值是( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | -$\frac{π}{4}$ | D. | -$\frac{π}{8}$ |
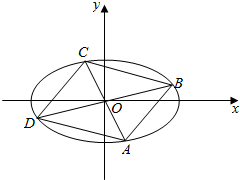 已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.
已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.