题目内容
12.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,若|($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$|=|($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$|,则( )| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$ | D. | $\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$ |
分析 根据数量积的意义,对已知等式去掉绝对值,分情况得到向量关系.
解答 解:因为$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,若|($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$|=|($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$|,
所以($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$,或者($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=-[($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$],
展开整理得到$\overrightarrow{b}•\overrightarrow{c}$=0,或者$\overrightarrow{a}•\overrightarrow{c}$=0,所以$\overrightarrow{b}⊥\overrightarrow{c}$或$\overrightarrow{a}⊥\overrightarrow{c}$;
故选D.
点评 本题考查了平面向量的数量积的运算;熟记数量积公式以及意义是解答的关键.

练习册系列答案
相关题目
2.若如图框图所给的程序运行结果为S=41,图中的判断框①中是i>a,则实数a的取值范围是( )
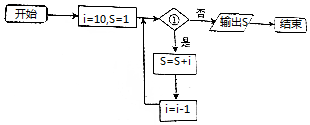

| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
3.从1,2,3,4,5这五个数字中选出三个不相同数组成一个三位数,则奇数位上必须是奇数的三位数个数为( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
7.执行如图所示的程序框图,输入的S0值为10时,则输出的S的值为( )


| A. | -4 | B. | 2 | C. | -20 | D. | 6 |
17.为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如表所示.
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价xi(单位:元/件,整数)和销量yi(单位:件)(i=1,2,…8)如表所示:
(ⅰ)请根据下列数据计算相应的相关指数R2,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价x定为多少时?利润z可以达到最大.
参考公式:相关指数M.
| 无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
| 本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
| 本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价xi(单位:元/件,整数)和销量yi(单位:件)(i=1,2,…8)如表所示:
| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
(ⅱ)根据所选回归模型,分析售价x定为多少时?利润z可以达到最大.
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
1.P(x,y)是曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$(0≤θ<π,θ是参数)上的动点,则$\frac{y}{x}$的取值范围是( )
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
2.定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,+∞) | D. | (0,+∞) |
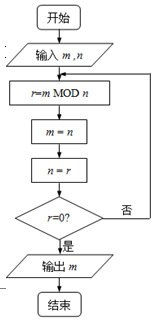 右边程序框图的算法思路源于数学名著《几何原本》中的“辗转
右边程序框图的算法思路源于数学名著《几何原本》中的“辗转