题目内容
已知在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则BC与平面ABC1所成的角的正弦值为 .
考点:直线与平面所成的角
专题:空间角
分析:如图所示,取AB的中点M,连接CM,C1M.由等边三角形的性质可得:CM⊥AB.CC1⊥AB,可得AB⊥平面C1MC,
因此∠CMC1二面角C-AB-C1的平面角,可得CM=
,C1M=
,CC1=
.过点C作CO⊥C1M,连接OB.AB⊥平面C1MC,可得平面ABC1⊥平面C1MC,CO⊥平面ABC1.∠OBC是BC与平面ABC1所成的角.利用直角三角形的边角关系即可得出.
因此∠CMC1二面角C-AB-C1的平面角,可得CM=
| ||
| 2 |
| 3 |
| 3 |
| 2 |
解答:
解:如图所示,取AB的中点M,连接CM,C1M.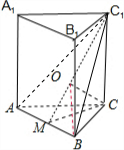
∵△ABC是等边三角形,
∴CM⊥AB.
又C1C⊥平面ABC,
∴CC1⊥AB.
又CM∩MC1=M,
∴AB⊥平面C1MC,
∴∠CMC1二面角C-AB-C1的平面角,其大小为60°.
∵AB=1,∴CM=
,
∴C1M=
,CC1=
.
过点C作CO⊥C1M,连接OB.
∵AB⊥平面C1MC,
∴平面ABC1⊥平面C1MC,
∴CO⊥平面ABC1.
∴∠OBC是BC与平面ABC1所成的角.
在△CMC1中,可得OC=
=
.
∴sin∠OBC=
=
.
故答案为:
.

∵△ABC是等边三角形,
∴CM⊥AB.
又C1C⊥平面ABC,
∴CC1⊥AB.
又CM∩MC1=M,
∴AB⊥平面C1MC,
∴∠CMC1二面角C-AB-C1的平面角,其大小为60°.
∵AB=1,∴CM=
| ||
| 2 |
∴C1M=
| 3 |
| 3 |
| 2 |
过点C作CO⊥C1M,连接OB.
∵AB⊥平面C1MC,
∴平面ABC1⊥平面C1MC,
∴CO⊥平面ABC1.
∴∠OBC是BC与平面ABC1所成的角.
在△CMC1中,可得OC=
| CM•CC1 |
| C1M |
| 3 |
| 4 |
∴sin∠OBC=
| OC |
| BC |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了空间角的求法、正三棱柱的性质、线面面面垂直的判定与性质定理、直角三角形的边角关系,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若向量
=(1,2)与向量
=(-1,x)平行,则x等于( )
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
关于直线l,m与平面α,β的命题中,一定正确的是( )
| A、若l∥m,m?α,则l∥α |
| B、若l⊥β,α⊥β,则l∥α |
| C、若l⊥β,α∥β,则l⊥α |
| D、若l?β,α⊥β,则l⊥α |
下列命题中,真命题是( )
| A、“a≤b”是“a+c≤b+c”的充分不必要条件 | ||||||||
| B、“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题 | ||||||||
| C、二进制数1010(2) 可表示为三进制数110(3) | ||||||||
D、“平面向量
|
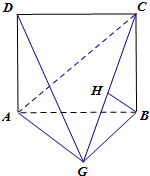 已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.
已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.