题目内容
15.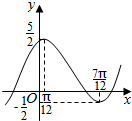 函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.(1)求f(x)的解析式;
(2)求f(x)的单调递增区间.
分析 (1)根据函数的最大值和最小值,算出A=1且k=$\frac{1}{2}$,再由函数的周期算出ω=$\frac{2π}{T}$=2,最后根据函数的最大值对应的x值,得到φ=$\frac{π}{3}$,可得f(x)的表达式.
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得f(x)的单调递增区间.
解答 解:(1)∵函数f(x)的最大值为$\frac{3}{2}$,最小值为-$\frac{1}{2}$,
∴2A=$\frac{3}{2}$-(-$\frac{1}{2}$)=2,得A=1,k=$\frac{1}{2}$[$\frac{3}{2}$+(-$\frac{1}{2}$)]=$\frac{1}{2}$,
∵函数的周期T=2($\frac{7π}{12}$-$\frac{π}{12}$)=π,
∴ω=$\frac{2π}{π}$=2.
而f($\frac{π}{12}$)=$\frac{3}{2}$为函数的最大值,得2×$\frac{π}{12}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
∴φ=$\frac{π}{3}$+2kπ,结合|φ|<$\frac{π}{2}$,得φ=$\frac{π}{3}$,
综上所述,得f(x)的表达式是f(x)=sin(2x+$\frac{π}{3}$)+$\frac{1}{2}$.
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得f(x)的单调递增区间为:[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈Z.
点评 本题给出三角函数图象满足的条件,求它的表达式,着重考查了三角函数的图象与性质和由y=Asin(ωx+φ)的部分图象确定其解析式等知识,属于基础题.

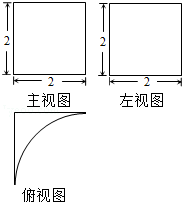 某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.
某几何体的三视图如图所示,其中俯视图为半径为2的四分之一个圆弧,则该几何体的体积为8-2π,表面积为16.