题目内容
6.已知函数$f(x)=1-\frac{4}{{2{a^x}+a}}(a>0,a≠1)$是定义在实数集R上的奇函数.(1)判断函数在R上的单调性并用定义证明你的结论;
(2)若方程f(x)-2m=0在R上有解,求实数m的范围;
(3)当x∈(0,1)时,mf(x)>2x-2恒成立,求实数m的取值范围.
分析 (1)由奇函数的性质f(0)=0,代入求出a,利用定义法判定即可;
(2)若方程f(x)-2m=0在R上有解,2m应在函数值域内,求出函数的值域即可;
(3)不等式可整理为(2x)2-(m+1)2x+m-2<0对x∈(0,1)恒成立,利用换元法令t=2x,
得t2-(m+1)t+m-2<0对于t∈(1,2)恒成立,利用二次不等式的性质可求出m的范围.
解答 解:(1)函数$f(x)=1-\frac{4}{{2{a^x}+a}}(a>0,a≠1)$是定义在实数集R上的奇函数,
∴f(0)=0,
∴a=2,
∴$f(x)=1-\frac{4}{{2{a^x}+a}}(a>0,a≠1)$
=1-$\frac{2}{{2}^{x}+1}$,
设x1<x2,则f(x2)-f(x1)=$\frac{2}{{2}^{{x}_{1}}+1}$-$\frac{2}{{2}^{{x}_{2}}+1}$
=$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{{(2}^{{x}_{2}}+1)({2}^{{x}_{1}}+1)}$
∵x1<x2,
∴2x1<2x2,即2x2-2x1>0,(2x1+1)(2x2+1)>0,
∴f(x2)-f(x1)=>0,
即f(x2)>f(x1),
∴f(x)是R上的递增函数.
(2)若方程f(x)-2m=0在R上有解,
∴1-$\frac{2}{{2}^{x}+1}$=2m有解,
∴2m应在函数值域内,
(Ⅱ)∵y=1-$\frac{2}{{2}^{x}+1}$
又∵2x>0,
∴2x+1>1
∴0<$\frac{2}{{2}^{x}+1}$<2,-1<1-$\frac{2}{{2}^{x}+1}$<1
∴函数f(x)的值域(-1,1),
∴m∈(-$\frac{1}{2}$,$\frac{1}{2}$);
(3)由题意,当x∈(0,1)时,mf(x)>2x-2恒成立,
即(2x)2-(m+1)2x+m-2<0对x∈(0,1)恒成立,
令t=2x,
∵x∈(0,1),
∴t∈(1,2),
∴t2-(m+1)t+m-2<0对于t∈(1,2)恒成立,
令g(t)=t2-(m+1)t+m-2,
∴g(1)<0,g(2)<0,
∴m>0.
点评 考查了奇函数的性质和单调性的证明,方程有解的问题和恒成立问题的转换.注意换元法的应用.

 作业辅导系列答案
作业辅导系列答案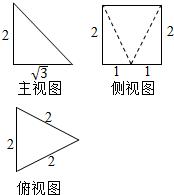
| A. | 4+$\sqrt{7}$ | B. | 8+$\sqrt{7}$ | C. | 4+$\sqrt{3}$+$\sqrt{7}$ | D. | 8+$\sqrt{3}$+$\sqrt{7}$ |
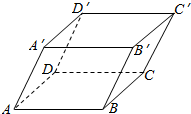 如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量:
如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量: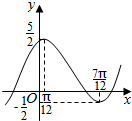 函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.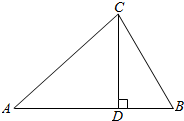 “如图,在△ABC中,AC>BC,CD是AB边上的高,求证:∠ACD>∠BCD”.
“如图,在△ABC中,AC>BC,CD是AB边上的高,求证:∠ACD>∠BCD”.