��Ŀ����
7�����������ĸ����⣺�ٺ���f��x��=|x|-1����ż���������ǣ�0��+�ޣ��ĵ���������������������x�IJ���ʽ|x-4|+|x+3|��a�Ľ⼯�ǿռ�����ʵ��a��ȡֵ��Χ�ǣ�-�ޣ�7����
��������f��x��=|x+1|+|x-a|��ͼ�����ֱ��x=2�Գƣ���a=5��
���躯��f��x��=$\left\{\begin{array}{l}{lg|x-2|��x��2��}\\{1��x=2��}\end{array}\right.$��������x�ķ���f2��x��+bf��x��+c=0��b��c��R��ǡ��5����ͬ��ʵ����x1��x2��x3��x4��x5����f��x1+x2+x3+x4+x5��=3lg2�����������������������Ǣ٢ۢܣ�
���� ��������f��x��=|x|-1�ĵ����Ժ���ż�ԣ����жϢ٣����|x-4|+|x+3|����Сֵ�����жϢڣ��������f��x��=|x+1|+|x-a|ͼ��Գ���ı���ʽ�����жϢۣ�����f��x1+x2+x3+x4+x5����ֵ�����жϢܣ�
��� �⣺�ٺ���f��x��=|x|-1������f��-x��=f��x������f��x����ż������
��x�ʣ�0��+�ޣ�ʱ��f��x��=|x|-1=x-1�ǵ�����������������ȷ��
��|x-4|+|x+3|��|��x-4��-��x+3��|=7��������x�IJ���ʽ|x-4|+|x+3|��a�Ľ⼯�ǿռ�����ʵ��a��ȡֵ��Χ�ǣ�-�ޣ�7]���ʴ���
��������f��x��=|x+1|+|x-a|��ͼ�����ֱ��x=2�Գƣ���$\frac{a-1}{2}=2$����a=5������ȷ��
���躯��f��x��=$\left\{\begin{array}{l}{lg|x-2|��x��2��}\\{1��x=2��}\end{array}\right.$��ͼ������ͼ��ʾ��
������x�ķ���f2��x��+bf��x��+c=0��b��c��R��ǡ��5����ͬ��ʵ����x1��x2��x3��x4��x5��
��x1+x2+x3+x4+x5=10��
��f��x1+x2+x3+x4+x5��=f��10��=3lg2������ȷ��
����ȷ�������Т٢ڢۢܣ�
�ʴ�Ϊ���٢ۢ�
���� ���������������ж���Ӧ��Ϊ���壬�����˺�������ż�ԣ������ԣ��Գ��Ե�֪ʶ�㣬�Ѷ��е���

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�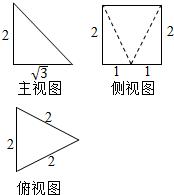
| A�� | 4+$\sqrt{7}$ | B�� | 8+$\sqrt{7}$ | C�� | 4+$\sqrt{3}$+$\sqrt{7}$ | D�� | 8+$\sqrt{3}$+$\sqrt{7}$ |
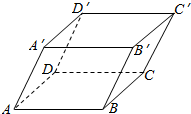 ��ͼ����֪ƽ��������ABCD-A��B��C��D�䣬�������и�����ʽ������ͼ�б����������������
��ͼ����֪ƽ��������ABCD-A��B��C��D�䣬�������и�����ʽ������ͼ�б����������������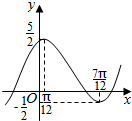 ����f��x��=Asin����x+�գ�+k��A��0���أ�0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ��
����f��x��=Asin����x+�գ�+k��A��0���أ�0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ��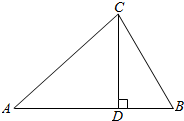 ����ͼ���ڡ�ABC�У�AC��BC��CD��AB���ϵĸߣ���֤����ACD����BCD����
����ͼ���ڡ�ABC�У�AC��BC��CD��AB���ϵĸߣ���֤����ACD����BCD����