题目内容
在平面直角坐标系xOy中,已知椭圆C:
+
=1(a>b>0)的离心率e=
,直线l:x-my-1=0(m∈R)过椭圆C的右焦点F,且交椭圆C于A,B两点.
(1)求椭圆C的标准方程;
(2)已知点D(
,0),连结BD,过点A作垂直于y轴的直线l1,设直线l1与直线BD交于点P,试探索当m变化时,是否存在一条定直线l2,使得点P恒在直线l2上?若存在,请求出直线l2的方程;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆C的标准方程;
(2)已知点D(
| 5 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题设,得
,及b2=a2-c2=3,即可得出.
(2)令m=0,则A(1,
),B(1, -
)或者A(1, -
),B(1,
).可得P(4,
)或P(4, -
),可知:满足题意的定直线l2只能是x=4.
只要证明点P恒在直线x=4上.设A(x1,y1),B(x2,y2),由于PA垂直于y轴,可得点P的纵坐标为y1,从而只要证明P(4,y1)在直线BD上. 利用根与系数的关系、斜率计算公式只要证明 kDB=kDP.
|
(2)令m=0,则A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
只要证明点P恒在直线x=4上.设A(x1,y1),B(x2,y2),由于PA垂直于y轴,可得点P的纵坐标为y1,从而只要证明P(4,y1)在直线BD上. 利用根与系数的关系、斜率计算公式只要证明 kDB=kDP.
解答:
解:(1)由题设,得
,解得
从而b2=a2-c2=3,
∴椭圆C的标准方程为
+
=1.
(2)令m=0,则A(1,
),B(1, -
)或者A(1, -
),B(1,
).
当A(1,
),B(1, -
)时,P(4,
);当A(1, -
),B(1,
)时,P(4, -
),
∴满足题意的定直线l2只能是x=4.
下面证明点P恒在直线x=4上.
设A(x1,y1),B(x2,y2),
由于PA垂直于y轴,∴点P的纵坐标为y1,从而只要证明P(4,y1)在直线BD上.
由
得(4+3m2)y2+6my-9=0,
∵△=144(1+m2)>0,
∴y1+y2=
,y1y2=
.①
∵kDB-kDP=
-
=
-
=
=
,
①式代入上式,得kDB-kDP=0,
∴kDB=kDP.
∴点P(4,y1)恒在直线BD上,从而直线l1、直线BD与直线l2:x=4三线恒过同一点P,
∴存在一条定直线l2:x=4使得点P恒在直线l2上.
|
|
从而b2=a2-c2=3,
∴椭圆C的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)令m=0,则A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴满足题意的定直线l2只能是x=4.
下面证明点P恒在直线x=4上.
设A(x1,y1),B(x2,y2),
由于PA垂直于y轴,∴点P的纵坐标为y1,从而只要证明P(4,y1)在直线BD上.
由
|
∵△=144(1+m2)>0,
∴y1+y2=
| -6m |
| 4+3m2 |
| -9 |
| 4+3m2 |
∵kDB-kDP=
| y2-0 | ||
x2-
|
| y1-0 | ||
4-
|
| y2 | ||
my2+1-
|
| y1 | ||
|
| ||||
|
y1+y2-
| ||
my2-
|
①式代入上式,得kDB-kDP=0,
∴kDB=kDP.
∴点P(4,y1)恒在直线BD上,从而直线l1、直线BD与直线l2:x=4三线恒过同一点P,
∴存在一条定直线l2:x=4使得点P恒在直线l2上.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、直线过定点问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
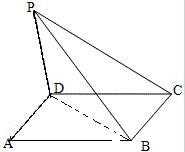 如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1:
如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1: