题目内容
15.已知$cos(\frac{π}{3}+α)=\frac{1}{3}$,则$sin(\frac{5}{6}π+α)$=( )| A. | .$\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | .$\frac{{2\sqrt{2}}}{3}$ | D. | .$-\frac{{2\sqrt{2}}}{3}$ |
分析 由已知利用诱导公式即可计算得解.
解答 解:∵$cos(\frac{π}{3}+α)=\frac{1}{3}$,
∴$sin(\frac{5}{6}π+α)$=sin[π-($\frac{5π}{6}$+α)]=sin($\frac{π}{6}$-α)=$cos(\frac{π}{3}+α)=\frac{1}{3}$.
故选:A
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
5.定义在R上的函数f(x)使不等式${f^'}(2x)>\frac{ln2}{2}f(2x)$恒成立,其中f'(x)是f(x)的导数,则( )
| A. | $\frac{f(2)}{f(0)}>2,\frac{f(0)}{{f({-2})}}>2$ | B. | f(2)>2f(0)>4f(-2) | C. | $\frac{f(2)}{f(0)}<2,\frac{f(0)}{{f({-2})}}<2$ | D. | f(2)<2f(0)<4f(-2) |
7.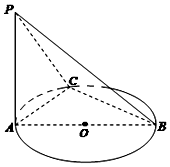 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
4.在数列{an}中,a1=1,${a_n}=1+\frac{1}{{{a_{n-1}}}}(n≥2)$,则a4=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{4}$ | D. | $\frac{8}{5}$ |