题目内容
在平面直角坐标系xOy中,已知圆心在x轴上,半径为4的圆C位于y轴的右侧,且与y轴相切,
(Ⅰ)求圆C的方程;
(Ⅱ)若椭圆
+
=1(b>0)的离心率为
,且左右焦点为F1,F2,试探究在圆C上是否存在点P,使得△PF1F2为直角三角形?若存在,请指出共有几个这样的P点?并说明理由(不必具体求出这些点的坐标)
(Ⅰ)求圆C的方程;
(Ⅱ)若椭圆
| x2 |
| 25 |
| y2 |
| b2 |
| 4 |
| 5 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)求圆C的方程,只要求出圆心与半径即可,而已知圆C的半径为4,圆心在x轴上,圆C位于y轴的右侧,且与y轴相切,故圆心为(4,0),从而可得圆C的方程;
(Ⅱ)假设存在满足条件的点P,根据椭圆方程可先求出F1,F2的坐标为(-4,0),(4,0),若△PF1F2为直角三角形,则过F2作x轴的垂线与圆交与两点,两点都满足题意,过F1作圆的切线,两个切点都满足题意.故有4个点符合题意.
(Ⅱ)假设存在满足条件的点P,根据椭圆方程可先求出F1,F2的坐标为(-4,0),(4,0),若△PF1F2为直角三角形,则过F2作x轴的垂线与圆交与两点,两点都满足题意,过F1作圆的切线,两个切点都满足题意.故有4个点符合题意.
解答:
解:(Ⅰ)∵圆心在x轴上,半径为4的圆C位于y轴的右侧,
∴可设圆的方程为(x-a)2+y2=16,(a>0)
∵圆与y轴相切,
∴a=4,
∴圆的方程为:(x-4)2+y2=16.
(Ⅱ)∵椭圆
+
=1(b>0)的离心率为
,
∴e=
=
=
,
解得:b=3
∴c=
=4,
∴F1(-4,0),F2(4,0)
∴F2(4,0)恰为圆心C.
①过F2作x轴的垂线与圆交与两点P1,P2,
则∠P1F2F1=∠P2F2F1=90°,
符合题意;
②过F1作圆的切线,分别与圆切于点P3,P4,
连接CP1,CP2,则∠F1P1F2=∠F1P2F2=90°.符合题意.
综上,圆C上存在4个点P,使得△PF1F2为直角三角形.
∴可设圆的方程为(x-a)2+y2=16,(a>0)
∵圆与y轴相切,
∴a=4,
∴圆的方程为:(x-4)2+y2=16.
(Ⅱ)∵椭圆
| x2 |
| 25 |
| y2 |
| b2 |
| 4 |
| 5 |
∴e=
| c |
| a |
| ||
| 5 |
| 4 |
| 5 |
解得:b=3
∴c=
| a2-b2 |
∴F1(-4,0),F2(4,0)
∴F2(4,0)恰为圆心C.
①过F2作x轴的垂线与圆交与两点P1,P2,
则∠P1F2F1=∠P2F2F1=90°,
符合题意;
②过F1作圆的切线,分别与圆切于点P3,P4,
连接CP1,CP2,则∠F1P1F2=∠F1P2F2=90°.符合题意.
综上,圆C上存在4个点P,使得△PF1F2为直角三角形.
点评:本题考查圆的方程,椭圆方程以及与椭圆相关的综合性问题,探索性问题的解决技巧等.属于难题.

练习册系列答案
相关题目
设Sn是等比数列{an}的前n项和,S4=5S2,则
的值为( )
| a3•a8 |
| a52 |
| A、-2或-1 | B、1或2 |
| C、±2或-1 | D、±1或2 |
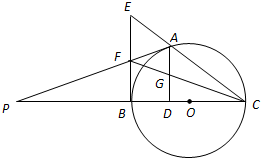 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.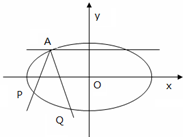 如图,焦点在x轴的椭圆,离心率e=
如图,焦点在x轴的椭圆,离心率e=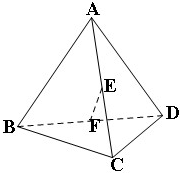 如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是
如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是