Question

15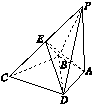．如图所示，PA与四边形ABCD所在平面垂直，且PA=BC=CD=BD，AB=AD，PD⊥DC．
（1）求证：AB⊥BC；
（2）若PA=$\sqrt{3}$，E为PC的中点，求三棱锥EABD的体积．

Answer 1

分析 （1）由已知得△PBC≌△PDC，则∠PBC=∠PDC，再由PD⊥DC，得PB⊥BC，由线面垂直的性质可得PA⊥BC，再由线面垂直的判定可得BC⊥平面PAB，从而得到AB⊥BC；
（2）由已知结合（1）得∠ABD=30°，解三角形求得AB=1，求出三角形ABD的面积，再求出三棱锥EABD的高h=$\frac{1}{2}PA=\frac{\sqrt{3}}{2}$，代入棱锥体积公式得答案．

解答 （1）证明：由PA⊥平面ABCD，AB=AD，可得PB=PD，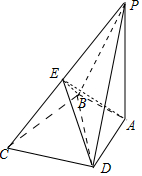
又BC=CD，∴△PBC≌△PDC，得∠PBC=∠PDC，
∵PD⊥DC，∴PB⊥BC，
∵PA⊥平面ABCD，BC?平面ABCD，∴PA⊥BC，
又PA∩PB=P，∴BC⊥平面PAB，
∵AB?平面PAB，∴AB⊥BC；
（2）解：由BC=CD=BD，AB⊥BC，可得∠ABD=30°，
由AB=AD，BD=PA=$\sqrt{3}$，可得AB=1，
∴△ABD的面积S=$\frac{1}{2}$×1×1×sin120°=$\frac{\sqrt{3}}{4}$．
∵E为PC的中点，∴三棱锥EABD的高h=$\frac{1}{2}PA=\frac{\sqrt{3}}{2}$，
故三棱锥EABD的体积V=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{\sqrt{3}}{2}=\frac{1}{8}$．

点评 本题考查直线与平面垂直的判定和性质，考查空间想象能力和思维能力，考查多面体体积的求法，是中档题．