题目内容
如图，四边形EFGH为空间四边形ABCD的一个截面，四边形EFGH为平行四边形．
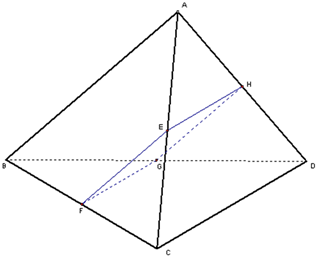
（1）求证：AB∥平面EFGH，CD∥平面EFGH；
（2）若AB=4，CD=6，AB，CD所成的角为60°，求四边形EFGH的面积的最大值．
（1）求证：AB∥平面EFGH，CD∥平面EFGH；
（2）若AB=4，CD=6，AB，CD所成的角为60°，求四边形EFGH的面积的最大值．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由已知条件推导出EF∥HG，从而得到EF∥平面ABD，进而得到EF∥AB，由此能证明AB∥平面EFGH，同理CD平面EFGH．
（2）由EF∥AB，EH∥CD，得到∠FEH或其补角即为AB，CD所成的角．由此能求出四边形EFGH的面积的最大值．
（2）由EF∥AB，EH∥CD，得到∠FEH或其补角即为AB，CD所成的角．由此能求出四边形EFGH的面积的最大值．
解答：
（1）证明：∵四边形EFGH为平行四边形，∴EF∥HG．
∵HG?平面ABD，EF不在平面ABC内，
∴EF∥平面ABD．…（2分）
∵EF?平面ABD，平面ABD∩平面ABC=AB，
∴EF∥AB．
∵EF?平面EFGH，AB不包含于平面EFGH，
∴AB∥平面EFGH，…（5分）
同理CD平面EFGH．…（6分）
（2）解：∵EF∥AB，EH∥CD，
∴∠FEH或其补角即为AB，CD所成的角．
设EF=x，EH=y．
由EF∥AB，EH∥CD，得
=
，
=
，
∴
+
=
+
=1，
∵AB=4，CD=6，∴
+
=1，∴y=6（1-
），
∴S△EFGH=xysin60°=
x•6(1-
)
=
[-(x-2)2+4]≤3
，
∴x=2时，四边形EFGH的面积有最大值是3
．
∵HG?平面ABD，EF不在平面ABC内，
∴EF∥平面ABD．…（2分）
∵EF?平面ABD，平面ABD∩平面ABC=AB，
∴EF∥AB．
∵EF?平面EFGH，AB不包含于平面EFGH，
∴AB∥平面EFGH，…（5分）
同理CD平面EFGH．…（6分）
（2）解：∵EF∥AB，EH∥CD，
∴∠FEH或其补角即为AB，CD所成的角．
设EF=x，EH=y．
由EF∥AB，EH∥CD，得
| EF |
| AB |
| CE |
| CA |
| EH |
| CD |
| AE |
| CA |
∴
| EF |
| AB |
| EH |
| CD |
| CE |
| CA |
| AE |
| CA |
∵AB=4，CD=6，∴
| x |
| 4 |
| y |
| 6 |
| x |
| 4 |
∴S△EFGH=xysin60°=
| ||
| 2 |
| x |
| 4 |
=
3
| ||
| 4 |
| 3 |
∴x=2时，四边形EFGH的面积有最大值是3
| 3 |
点评：本题考查直线与平面平行的证明，考查四边形面积最大值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知：正方形ABCD与正方形ABEF不共面，N、M分别在AE和BD上，AN=DM．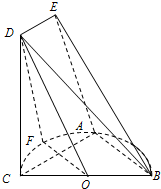
如图：已知BC是半径为1的半圆O的直径，A是半圆周上不同于B，C的点，F为弧AC的中点．在梯形ACDE中，DE∥AC且AC=2DE，平面ACDE⊥平面ABC．求证：