题目内容
选修4-2:矩阵与变换
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量
=(
),并有特征值λ2=-1及属于特征值-1的一个特征向量
=(
),
=(
).
(1)求矩阵M;
(2)求M5α.
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量
| e1 |
2 3 |
| e2 |
1 -1 |
| α |
-1 1 |
(1)求矩阵M;
(2)求M5α.
考点:特征值、特征向量的应用
专题:选作题,矩阵和变换
分析:(1)利用待定系数法,即可求矩阵M;
(2)确定α=0
+(-1)
,即可求M5α.
(2)确定α=0
|
|
解答:
解:(1)设M=
则
=4
,∴
①
又
=(-1)
,∴
②
由①②可得a=1,b=2,c=3,d=2,∴M=
.…(4分)
(2)易知α=0
+(-1)
,∴M5α=(-1)6α=
…(7分)
|
则
|
|
|
|
又
|
|
|
|
由①②可得a=1,b=2,c=3,d=2,∴M=
|
(2)易知α=0
|
|
|
点评:本题考查矩阵的性质和应用、特征值与特征向量的计算,解题时要注意特征值与特征向量的计算公式的运用.

练习册系列答案
相关题目
下列语句不是命题的是( )
| A、5>8 | ||
B、若a是正数,则
| ||
| C、x∈{-1,0,1,2} | ||
| D、正弦函数是奇函数 |
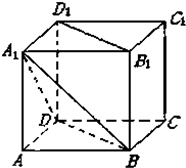 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,