题目内容
已知以点C（1，-2）为圆心的圆与直线x+y-1=0相切．
（1）求圆C的标准方程；
（2）求过圆内一点P（2，-
）的最短弦所在直线的方程．
（1）求圆C的标准方程；
（2）求过圆内一点P（2，-
| 5 |
| 2 |
考点：直线和圆的方程的应用,圆的标准方程
专题：综合题,直线与圆
分析：（1）由点到直线的距离求出半径，从而得到圆的方程；
（2）由垂径定理可得，过P点的最短弦所在直线与过P点的直径垂直，求出过P点的直径的斜率，进而求出过P点的最短弦所在直线的斜率，利用点斜式，可以得到过P点的最短弦所在直线的方程．
（2）由垂径定理可得，过P点的最短弦所在直线与过P点的直径垂直，求出过P点的直径的斜率，进而求出过P点的最短弦所在直线的斜率，利用点斜式，可以得到过P点的最短弦所在直线的方程．
解答：
解：（1）圆的半径r=
=
，
所以圆的方程为（x-1）2+（y+2）2=2．
（2）圆的圆心坐标为C（1，-2），则过P点的直径所在直线的斜率为-
，
由于过P点的最短弦所在直线与过P点的直径垂直
∴过P点的最短弦所在直线的斜率为2，
∴过P点的最短弦所在直线的方程y+
=2（x-2），即4x-2y-13=0．
| |1-2-1| | ||
|
| 2 |
所以圆的方程为（x-1）2+（y+2）2=2．
（2）圆的圆心坐标为C（1，-2），则过P点的直径所在直线的斜率为-
| 1 |
| 2 |
由于过P点的最短弦所在直线与过P点的直径垂直
∴过P点的最短弦所在直线的斜率为2，
∴过P点的最短弦所在直线的方程y+
| 5 |
| 2 |
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．由垂径定理，判断出过P点的最短弦所在直线与过P点的直径垂直是解答本题的关键．
练习册系列答案
相关题目
tan（α+β）=
，tan（α-β）=
，则tan2α=（ ）
| 2 |
| 5 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
命题“?x∈R，x2+2x+3
≥0”的否定为（ ）
| 2 |
A、?x0∈R，x02+2x0+3
| ||
B、?x0∈R，x02+2x0+3
| ||
C、?x∈R，x2+2x+3
| ||
D、?x∈R，x2+2x+3
|
函数y=lgx2的单调减区间为（ ）
| A、R |
| B、（-∞，0），（0，+∞） |
| C、（-∞，0） |
| D、（0，+∞） |
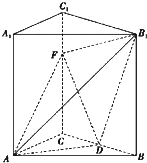在直三棱柱ABC-A1B1C1中，AB=AC=AA1=3，BC=2，D是BC的中点，F是C1C上一点．
如图，AB是圆O的直径，BC是圆O的切线，切点为B，OC平行于弦AD．