题目内容
命题“?x∈R，x2+2x+3
≥0”的否定为（ ）
| 2 |
A、?x0∈R，x02+2x0+3
| ||
B、?x0∈R，x02+2x0+3
| ||
C、?x∈R，x2+2x+3
| ||
D、?x∈R，x2+2x+3
|
考点：命题的否定
专题：简易逻辑
分析：利用全称命题的否定是特称命题写出结果即可．
解答：
解：全称命题的否定是特称命题，
所以命题“?x∈R，x2+2x+3
≥0”的否定为：?x0∈R，x02+2x0+3
＜0．
故选：A．
所以命题“?x∈R，x2+2x+3
| 2 |
| 2 |
故选：A．
点评：本题考查命题的否定，注意全称命题与特称命题的否定关系．
练习册系列答案
相关题目
已知复数z=
，则（ ）
| 2 |
| -1+i |
| A、z的虚部为-1 |
| B、z的实部为1 |
| C、|z|=2 |
| D、z的共轭复数为1+i |
2014年索契冬季奥运会的花样滑冰项目上，8个评委为某选手打出的分数如茎叶图所示，则这些数据的中位数是（ ）| A、84 | B、85 |
| C、86 | D、87.5 |
已知点P（-1，1）与点Q（3，5）关于直线l对称，则直线l的方程为（ ）
| A、x-y+1=0 |
| B、x+y=0 |
| C、x+y-4=0 |
| D、x-y=0 |
直线xcosα+ysinα+1=0，α∈（0，
）的倾斜角为（ ）
| π |
| 2 |
| A、α | ||
B、
| ||
| C、π-α | ||
D、
|
直线l过点P（1，3），且与x、y轴正半轴围成的三角形的面积等于6的直线方程是（ ）
| A、3x+y-6=0 |
| B、x+3y-10=0 |
| C、3x-y=0 |
| D、x-3y+8=0 |
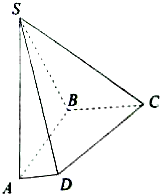如图所示，在四棱锥S-ABCD中，底面ABCD是直角梯形，SA⊥平面ABCD，且AD∥BC，AB⊥AD，BC=2AD=2，AB=AS=