题目内容
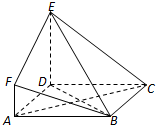 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求平面BEF与平面BED夹角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得DE⊥AC,AC⊥BD,由此能证明AC⊥平面BDE.
(Ⅱ)以D为原点建立空间直角直角坐标系D-xyz,利用向量法能求出平面BEF与平面BED夹角的余弦值.
(Ⅱ)以D为原点建立空间直角直角坐标系D-xyz,利用向量法能求出平面BEF与平面BED夹角的余弦值.
解答:
(Ⅰ)证明:因为DE⊥平面ABCD,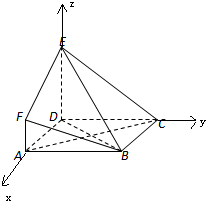
所以DE⊥AC,(2分)
因为ABCD是正方形,所以AC⊥BD,
又DE∩BD=D,所以AC⊥平面BDE.(4分)
(Ⅱ)解:因为DA,DC,DE两两垂直,
所以以D为原点建立空间直角直角坐标系D-xyz,
因为BE与平面ABCD所成角为60°,
即∠BDE=60°,(6分)所以
=
.
由AD=3可知DE=3
,AF=
则A(3,0,0),F(3,0,
),E(0,0,3
),
B(3,3,0),C(0,3,0),
所以
=(0,-3,
),
=(3,0,-2
)
设平面BEF的法向量为
=(x,y,z),
则
,即
,
令z=
,则
=(4,2,
)
因为AC⊥平面BDE,所以
为平面BDE的法向量,
=(3,-3,0),
所以cos<
,
>=
=
=
.
所以平面BEF与平面BED夹角的余弦为
.(12分)

所以DE⊥AC,(2分)
因为ABCD是正方形,所以AC⊥BD,
又DE∩BD=D,所以AC⊥平面BDE.(4分)
(Ⅱ)解:因为DA,DC,DE两两垂直,
所以以D为原点建立空间直角直角坐标系D-xyz,
因为BE与平面ABCD所成角为60°,
即∠BDE=60°,(6分)所以
| ED |
| DB |
| 3 |
由AD=3可知DE=3
| 6 |
| 6 |
则A(3,0,0),F(3,0,
| 6 |
| 6 |
B(3,3,0),C(0,3,0),
所以
| BF |
| 6 |
| EF |
| 6 |
设平面BEF的法向量为
| n |
则
|
|
令z=
| 6 |
| n |
| 6 |
因为AC⊥平面BDE,所以
| CA |
| CA |
所以cos<
| n |
| CA |
| ||||
|
|
| 6 | ||||
3
|
| ||
| 13 |
所以平面BEF与平面BED夹角的余弦为
| ||
| 13 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
化简cos(45°-α)cos(α+15°)-sin(45°-α)sin(α+15°)的结果是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式x[f(x)-f(-x)]<0的解集为( )
| A、(-1,0)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
设M={0,1,2,4,5,8},N={0,2,3,5},则N∩M=( )
| A、{1,3} |
| B、{1,4,8} |
| C、{0,2,5} |
| D、{2,4,6} |
若实数x,y满足
,若z=x+2y,则z的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点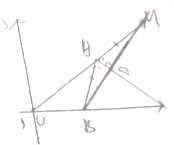 如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.
如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.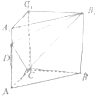 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.