题目内容
设i为虚数单位,复数
的共轭复数是( )
| 2i |
| 1-2i |
A、
| ||||
B、-
| ||||
| C、i | ||||
D、-
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:根据复数的概念以及基本运算进行求解.
解答:
解:
=
=
=-
+
i,
则复数
的共轭复数是-
-
i,
故选:D
| 2i |
| 1-2i |
| 2i(1+2i) |
| (1-2i)(1+2i) |
| 2i-4 |
| 1+4 |
| 4 |
| 5 |
| 2 |
| 5 |
则复数
| 2i |
| 1-2i |
| 4 |
| 5 |
| 2 |
| 5 |
故选:D
点评:本题主要考查复数的基本运算,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
化简cos(45°-α)cos(α+15°)-sin(45°-α)sin(α+15°)的结果是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如果扇形圆心角的弧度数为2,圆心角所对的弦长也为2,那么这个扇形的面积是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式x[f(x)-f(-x)]<0的解集为( )
| A、(-1,0)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
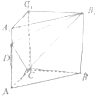 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.