题目内容
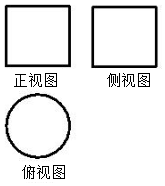
4．一个正三棱柱的主视图如图所示，则其左视图的面积（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
分析 根据正三棱柱的主视图确定出三棱柱的底面边长与高，即可求出左视图的面积．
解答 解：由主视图
知：三棱柱是以底面边长为2，高为1的正三棱柱，
左视图是矩形，边长为：$\sqrt{3}$和1，左视图的面积为$\sqrt{3}$×1=$\sqrt{3}$，
故选：C．
点评 此题考查了由三视图求面积、体积，确定出三棱柱的左视图的底边边长与高是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．一个几何体的正视图，侧视图为边长为2的正方形，其全面积为（ ）
| A． | 6π | B． | $8\sqrt{2}$π | C． | $4+4\sqrt{2}$π | D． | $8+4\sqrt{2}$π |
11．已知z=1-i（i是虚数单位），$\frac{i}{\overline{z}}$表示的点落在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
8．下列四组函数中，表示同一函数的是（ ）
| A． | f（x）=|x|和g（x）=$\sqrt{{x}^{2}}$ | B． | f（x）=$\sqrt{{x}^{2}}$和 g（x）=（$\sqrt{x}$）2 | ||
| C． | f（x）=$\frac{{x}^{2}-1}{x-1}$和g（x）=x+1 | D． | f（x）=x-1与g（x）=$\frac{{x}^{2}}{x}$-1 |
