题目内容
14.若“x2+2x-3>0”是“x<a”的必要不充分条件,则实数a的最大值为-3.分析 因x2+2x-3>0得x<-3或x>-1,又“x2-2x-3>0”是“x<a”的必要不充分条件,知“x<a”可以推出“x2-2x-3>0”,反之不成立,由此可求出a的最大值.
解答 解;∵“x2+2x-3>0”
∴x<-3或x>1,
∵“x2-2x-3>0”是“x<a”的必要不充分条件
∴(-∞,a)?(-∞,-3)∪(1,+∞)
∴a≤-3
故答案为:-3
点评 本题考查必要条件、充分条件、充要条件的判断,解题时要认真审题,仔细解答,属于基础题

练习册系列答案
相关题目
6.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且当$x∈[0,\frac{π}{2})$时,f(x)=sinx,则$f(\frac{8}{3}π)$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
4.一个正三棱柱的主视图如图所示,则其左视图的面积( )


| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
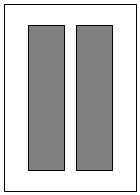 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm