题目内容
11．已知z=1-i（i是虚数单位），$\frac{i}{\overline{z}}$表示的点落在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 由已知z，求出$\overline{z}$，然后代入$\frac{i}{\overline{z}}$，再利用复数代数形式的乘除运算化简去，求出$\frac{i}{\overline{z}}$表示的点的坐标，则答案可求．
解答 解：∵z=1-i，
∴$\overline{z}=1+i$．
则$\frac{i}{\overline{z}}$=$\frac{i}{1+i}=\frac{i（1-i）}{（1+i）（1-i）}=\frac{1+i}{2}=\frac{1}{2}+\frac{1}{2}i$，
∴$\frac{i}{\overline{z}}$表示的点的坐标为：（$\frac{1}{2}$，$\frac{1}{2}$），位于第一象限．
故选：A．
点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
6．定义在R上的函数f（x）既是奇函数又是周期函数，若f（x）的最小正周期是π，且当$x∈[0，\frac{π}{2}）$时，f（x）=sinx，则$f（\frac{8}{3}π）$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
4．一个正三棱柱的主视图如图所示，则其左视图的面积（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
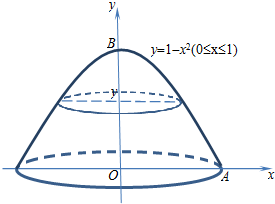在xOy平面上，将抛物线弧y=1-x2（0≤x≤1）、x轴、y轴围成的封闭图形记为D，如图中曲边三角形OAB及内部．记D绕y轴旋转一周而成的几何体为Ω，过点（0，y）（0≤y≤1）作Ω的水平截面，所得截面面积为（1-y）π，试构造一个平放的直三棱柱，利用祖暅原理得出Ω的体积值为$\frac{π}{2}$．