题目内容
9.已知数列{an}的前n项和为Sn,且$\frac{1}{{{a_n}+1}}=\frac{3}{{{a_{n+1}}+1}},{a_2}=5$,则Sn=3n-n-1.分析 $\frac{1}{{{a_n}+1}}=\frac{3}{{{a_{n+1}}+1}},{a_2}=5$,可得:$\frac{{a}_{n+1}+1}{{a}_{n}+1}$=3,a1=1.再利用等比数列的通项公式与求和公式即可得出.
解答 解:∵$\frac{1}{{{a_n}+1}}=\frac{3}{{{a_{n+1}}+1}},{a_2}=5$,
∴$\frac{{a}_{n+1}+1}{{a}_{n}+1}$=3,a1=1.
∴数列{an+1}是等比数列,公比为3,首项为2.
∴an+1=2×3n-1,即an=2×3n-1-1,
∴Sn=$2×\frac{{3}^{n}-1}{3-1}$-n=3n-n-1.
故答案为:3n-n-1.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知集合A={x|2x>1},B={x|log2x<0},则∁AB=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
18.已知x>y>0,则( )
| A. | $\frac{1}{x}-\frac{1}{y}>0$ | B. | sinx-siny>0 | C. | ${({\frac{1}{2}})^x}-{({\frac{1}{2}})^y}<0$ | D. | lnx+lny>0 |
19.执行如图所示的程序框图,若m=8,则输出的结果是( )
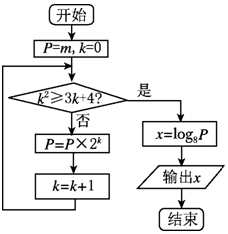

| A. | 2 | B. | $\frac{7}{3}$ | C. | 3 | D. | $\frac{13}{3}$ |
