题目内容
(1)求右焦点坐标是(2,0),且经过点(-2,-
)的椭圆的标准方程.
(2)已知双曲线与椭圆
+
=1共焦点,且以y=±
x为渐近线,求双曲线方程.
| 2 |
(2)已知双曲线与椭圆
| x2 |
| 49 |
| y2 |
| 24 |
| 4 |
| 3 |
考点:双曲线的标准方程,椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用待定系数法,即可求出椭圆的标准方程.
(2)求出椭圆
+
=1焦点,设出双曲线方程,建立方程组,即可求双曲线方程.
(2)求出椭圆
| x2 |
| 49 |
| y2 |
| 24 |
解答:
解:(1)设椭圆的标准方程为
+
=1,a>b>0,
∵a2=b2+4,
∴椭圆的方程为
+
=1,
∵点(-2,-
)在椭圆上,
∴
+
=1,解得 b2=4或b2=-2(舍),
由此得a2=8,即椭圆的标准方程为
+
=1.
(2)由椭圆
+
=1⇒c=5.
设双曲线方程为
-
=1,则
⇒
,
故所求双曲线方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵a2=b2+4,
∴椭圆的方程为
| x2 |
| b2+4 |
| y2 |
| b2 |
∵点(-2,-
| 2 |
∴
| 4 |
| b2+4 |
| 2 |
| b2 |
由此得a2=8,即椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)由椭圆
| x2 |
| 49 |
| y2 |
| 24 |
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
|
故所求双曲线方程为
| x2 |
| 9 |
| y2 |
| 16 |
点评:本题考查椭圆、双曲线的标准方程,考查待定系数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
sin
的值是( )
| 11π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 如图,在△ABC中,∠ACB是直角,D是AB的中点,F是CD的中点,求
如图,在△ABC中,∠ACB是直角,D是AB的中点,F是CD的中点,求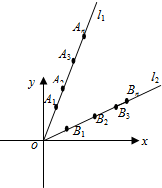 已知直线l1:y=3x,l2:y=
已知直线l1:y=3x,l2:y=