题目内容

sin
11π
6
的值是（　　）
A、
1
2
B、-
1
2
C、
3
2
D、-
3
2
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用诱导公式易求sin
11π
6
=-sin
π
6
=-
1
2
，从而可得答案．
解答： 解：sin
11π
6
=sin（2π-
π
6
）=-sin
π
6
=-
1
2
，
故选：B．
点评：本题考查运用诱导公式化简求值，属于基础题．
练习册系列答案
相关题目
已知（
1
9
）x+（
1
3
）x-1+a=0有正解，则a的取值范围是
 
．
方程lnx-x+2=0的根的个数是
 
．
下列命题错误的是（　　）
A、已知数列{an}为等比数列，若m+n=p+q，m，n，p，q∈N*，则有am•an=ap•aq
B、点（
π
8
，0）为函数f（x）=tan（2x+
π
4
）图象的一个对称中心
C、若
∫
a
0
x2=
8
3
，则a=2
D、若|
a
|=1，|
b
|=2，向量
a
与向量
b
的夹角为120°，则
b
在向量
a
上的投影为1
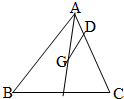
如图所示，在△ABC中，G为△ABC的重心，D在边AC上，且
CD
=3
DA
，则（　　）
A、
GD
=
1
3
AB
+
7
12
AC
B、
GD
=-
1
3
AB
-
1
12
AC
C、
GD
=-
1
3
AB
+
7
12
AC
D、
GD
=-
1
3
AB
+
1
12
AC
指数函数f（x）=（a-1）x在R上是增函数，则a的取值范围是（　　）
A、a＞1B、a＞2
C、0＜a＜1D、1＜a＜2
已知sinθ=-
12
13
，θ∈（-
π
2
，0），则cos（θ-
π
4
）的值为（　　）
A、-
7
2
26
B、
7
2
26
C、-
17
2
26
D、
17
2
26
若实数a，b，c，d满足
a2-2lna
b
=
3c-4
d
=1，则（a-c）2+（b-d）2的最小值为（　　）
A、
2(1-ln2)
5
B、
2(1+ln2)
5
C、
2
(1-ln2)
5
D、
2(1-ln2)2
5
（1）求右焦点坐标是（2，0），且经过点（-2，-
2
）的椭圆的标准方程．
（2）已知双曲线与椭圆
x2
49
+
y2
24
=1共焦点，且以y=±
4
3
x为渐近线，求双曲线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网