题目内容
△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC.
(Ⅰ)求cosA;
(Ⅱ)若a=3,△ABC的面积为2
,且b>c,求b,c.
(Ⅰ)求cosA;
(Ⅱ)若a=3,△ABC的面积为2
| 2 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)已知等式左边第一项利用两角和与差的余弦函数公式化简,整理后求出cos(B+C)的值,再利用诱导公式变形即可求出cosA的值;
(Ⅱ)利用三角形面积公式列出关系式,将sinA与已知面积代入得到bc=6,再利用余弦定理列出关系式,将a,bc,cosA的值代入得到b2+c2=13,联立即可求出b与c的值.
(Ⅱ)利用三角形面积公式列出关系式,将sinA与已知面积代入得到bc=6,再利用余弦定理列出关系式,将a,bc,cosA的值代入得到b2+c2=13,联立即可求出b与c的值.
解答:
解:(Ⅰ)由题意得:3cos(B-C)-1=3(cosBcosC+sinBsinC)-1=6cosBcosC,
整理得:3(-cosBcosC+sinBsinC)=1,即cos(B+C)=-
,
则cosA=-cos(B+C)=
;
(II)由(Ⅰ)得sinA=
=
,
∵△ABC面积为2
,即
bcsinA=
bc•
=2
,
∴bc=6①,
∵a=3,cosA=
,bc=6,
∴由余弦定理得:cosA=
=
=
,即b2+c2=13②,
联立①②,解得:
或
(舍),
则b=3,c=2.
整理得:3(-cosBcosC+sinBsinC)=1,即cos(B+C)=-
| 1 |
| 3 |
则cosA=-cos(B+C)=
| 1 |
| 3 |
(II)由(Ⅰ)得sinA=
| 1-cos2A |
2
| ||
| 3 |
∵△ABC面积为2
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
∴bc=6①,
∵a=3,cosA=
| 1 |
| 3 |
∴由余弦定理得:cosA=
| b2+c2-a2 |
| 2bc |
| b2+c2-9 |
| 12 |
| 1 |
| 3 |
联立①②,解得:
|
|
则b=3,c=2.
点评:此题考查了正弦、余弦定理,三角形的面积公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
如图所示,在△ABC中,G为△ABC的重心,D在边AC上,且
=3
,则( )
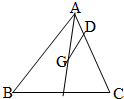
| CD |
| DA |

A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知不等式f(x)=
sin
cos
+cos2
-
-m≤0对于任意的-
≤x≤
恒成立,则实数m的取值范围是( )
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 6 |
A、m≥
| ||||||||
B、m≤
| ||||||||
C、m≤-
| ||||||||
D、-
|
 (1)求值(0.064)
(1)求值(0.064)