题目内容
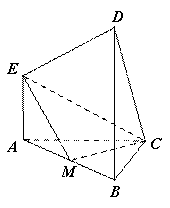
在如图所示的多面体中,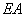 ⊥平面
⊥平面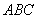 ,
,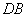 ⊥平面ABC,
⊥平面ABC,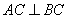 ,且
,且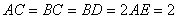 ,
,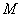 是
是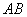 的中点.
的中点.
(Ⅰ)求证: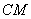 ⊥
⊥ ;
;
(Ⅱ)求平面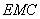 与平面
与平面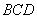 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(Ⅲ)在棱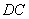 上是否存在一点
上是否存在一点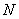 ,使得直线
,使得直线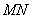 与平面
与平面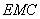 所成的角为
所成的角为 .若存在,指出点
.若存在,指出点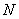 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(I)证明:  是
是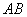 的中点
的中点 .
.
又
 平面
平面 ,
, .
.
 平面
平面
∴ ………………4分
………………4分
(Ⅱ)以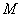 为原点,分别以
为原点,分别以 ,
, 为x,y轴,如图建立坐标系
为x,y轴,如图建立坐标系 ,
,
则

设平面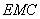 的一个法向量
的一个法向量 ,则
,则
取 所以
所以
设平面 的一个法向量
的一个法向量 ,则
,则
取 ,所以
,所以

所以平面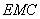 与平面
与平面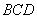 所成的锐二面角的余弦值
所成的锐二面角的余弦值 . ………………9分
. ………………9分
(Ⅲ)设 且
且 ,
,


若直线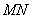 与平面
与平面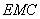 所成的角为
所成的角为 ,则
,则

解得: ,所以符合条件的点
,所以符合条件的点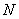 存在,为棱
存在,为棱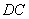 的中点. ………………14
的中点. ………………14

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则其最小正周期和图象的一条对称轴方程分别为( )
,则其最小正周期和图象的一条对称轴方程分别为( ) B.
B. C.
C. D.
D.
 ,
, ,则
,则
 B.
B.  C.
C.  D.
D. 
 是各项均为正数的等差数列,首项
是各项均为正数的等差数列,首项 ,其前
,其前 项和为
项和为 ,数列
,数列 是等比数列,首项
是等比数列,首项 ,且
,且 .
. ,其中
,其中 ,求数列
,求数列 的前
的前 项和
项和 .
. 的焦点为F,准线为
的焦点为F,准线为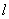 ,P是
,P是 ,则
,则
 满足
满足

 是虚数单位
是虚数单位 ,则
,则 B.
B. C.
C. D.
D.
 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .若
.若 ,则
,则 的最小值为
的最小值为 是第二象限角,且
是第二象限角,且 ,则
,则
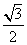 B.
B. C.
C. D.
D.
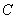 :
: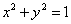 ,将曲线
,将曲线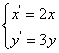 得到曲线
得到曲线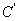 ;以直角坐标系原点为极点,
;以直角坐标系原点为极点,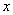 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线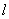 的极坐标系方程是
的极坐标系方程是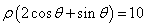 。
。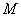 到直线
到直线