题目内容
8.已知$α∈(\frac{π}{2},π)$,且sin(π+α)=-$\frac{3}{5}$,则tanα=( )| A. | $-\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
分析 已知等式左边利用诱导公式化简求出sinα的值,利用同角三角函数间的基本关系求出cosα的值,进而确定出tanα的值.
解答 解:∵α∈($\frac{π}{2}$,π),sin(π+α)=-sinα=-$\frac{3}{5}$,即sinα=$\frac{3}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,
则tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
故选:A.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某几何体的三视图如图所示,则其表面积为( )
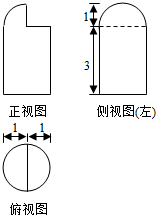

| A. | $\frac{17π}{2}$ | B. | 9π | C. | $\frac{19π}{2}$ | D. | 10π |
13.“x>2“是“x2+2x-8>0“成立的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.如果执行如所示的程序框图,那么输出的S=( )


| A. | 119 | B. | 600 | C. | 719 | D. | 4949 |
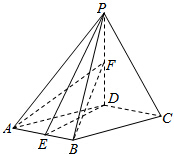 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.