题目内容
已知椭圆O：
+
=1的离心率为e1，动△ABC是其内接三角形，且
=
+
．若AB的中点为D，D的轨迹E的离心率为e2，则（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| A、e1=e2 |
| B、e1＜e2 |
| C、e1＞e2 |
| D、e1e2=1 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设A（x1，y1），B（x2，y2），代入椭圆的方程并利用
=
+
，可得C(
x1+
x2，
y1+
y2)．代入椭圆的方程可得
+
=0（定值）．再利用中点坐标公式可得D的坐标，计算
+
为定值即可得出．
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| x1x2 |
| a2 |
| y1y2 |
| b2 |
| ||
| a2 |
| ||
| b2 |
解答：
解：设A（x1，y1），B（x2，y2），
则
+
=1，
+
=1
由
=
+
，得C(
x1+
x2，
y1+
y2)．
∵C是椭圆上一点，
∴
+
=1，
(
)2(
+
)+(
)2(
+
)+2(
)(
)(
+
)=1，
得
+
=0（定值）．
设D(x，y)，则x=
，y=
，
∴
+
=
+
=
(
+
)+
(
+
)=
，
∴e1=e2．
故选：A．
则
| ||
| a2 |
| ||
| b2 |
| ||
| a2 |
| ||
| b2 |
由
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∵C是椭圆上一点，
∴
(
| ||||
| a2 |
(
| ||||
| b2 |
(
| 3 |
| 5 |
| ||
| a2 |
| ||
| b2 |
| 4 |
| 5 |
| ||
| a2 |
| ||
| b2 |
| 3 |
| 5 |
| 4 |
| 5 |
| x1x2 |
| a2 |
| y1y2 |
| b2 |
得
| x1x2 |
| a2 |
| y1y2 |
| b2 |
设D(x，y)，则x=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∴
| x2 |
| a2 |
| y2 |
| b2 |
(
| ||
| a2 |
(
| ||
| b2 |
| 1 |
| 4 |
| ||
| a2 |
| ||
| b2 |
| 1 |
| 4 |
| ||
| a2 |
| ||
| b2 |
| 1 |
| 2 |
∴e1=e2．
故选：A．
点评：本题考查了点与椭圆的位置关系、椭圆的性质、向量的坐标运算和数乘运算、中点坐标公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
有四辆不同特警车准备进驻四个编号为1，2，3，4的人群聚集地，其中有一个地方没有特警车的方法共（ ）种．
| A、144 | B、182 |
| C、106 | D、170 |
复数||z+i|-|z-i||=2对应复平面内的曲线是（ ）
| A、双曲线 | B、双曲线的一支 |
| C、线段 | D、两条射线 |
记A=cos
，B=cos
，C=sin
-sin
，则A，B，C的大小关系是（ ）
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、A＞B＞C |
| B、A＞C＞B |
| C、B＞A＞C |
| D、C＞B＞A |
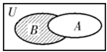已知全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，则图中阴影部分所表示的集合是（ ）| A、{1，2，4} |
| B、{3，7，8} |
| C、{1，2，4，6} |
| D、{3，6，7，8} |
对于区间[a，b]上有意义的两个函数f（x）与g（x），如果对于区间[a，b]中的任意数x均有|f（x）-g（x）|≤1，则称函数f（x）与g（x）在区间[a，b]上是密切函数，[a，b]称为密切区间．若m（x）=x2-3x+4与n（x）=2x-3在某个区间上是“密切函数”，则它的一个密切区间可能是（ ）
| A、[3，4] |
| B、[2，4] |
| C、[1，4] |
| D、[2，3] |
若平面α的法向量为
1=(3，2，1)，平面β的法向量为
=(-2，0，1)，则平面α与β夹角（锐角）的余弦是（ ）
| n |
| n2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|