题目内容
平面内有n个圆，其中每两个圆都相交于两点，且每三个圆都不共点，用f（n）表示这n个圆把平面分割的区域数，那么f（n+1）与f（n）之间的关系为（ ）
| A、f（n+1）=f（n）+n |
| B、f（n+1）=f（n）+2n |
| C、f（n+1）=f（n）+n+1 |
| D、f（n+1）=f（n）+n-1 |
考点：归纳推理
专题：规律型,推理和证明
分析：我们由两个圆相交将平面分为4分，三个圆相交将平面分为8分，四个圆相交将平面分为14部分，我们进行归纳推理，易得到结论．
解答：
解：∵一个圆将平面分为2份
两个圆相交将平面分为4=2+2份，
三个圆相交将平面分为8=2+2+4份，
四个圆相交将平面分为14=2+2+4+6份，
…
平面内n个圆，其中每两个圆都相交于两点，且任意三个圆不相交于同一点，
则该n个圆分平面区域数f（n）=2+（n-1）n=n2-n+2
∴f（n+1）=f（n）+2n，
故选：B
两个圆相交将平面分为4=2+2份，
三个圆相交将平面分为8=2+2+4份，
四个圆相交将平面分为14=2+2+4+6份，
…
平面内n个圆，其中每两个圆都相交于两点，且任意三个圆不相交于同一点，
则该n个圆分平面区域数f（n）=2+（n-1）n=n2-n+2
∴f（n+1）=f（n）+2n，
故选：B
点评：本题主要考查了进行简单的合情推理．归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
在△ABC的三个内角之比为3：2：1，那么对应的三边之比为（ ）
| A、3：2：1 | ||||
B、
| ||||
C、
| ||||
D、2：
|
函数f（x）=
x-cosx的零点个数为（ ）
| 1 |
| 8 |
| A、3 | B、4 | C、5 | D、6 |
过双曲线x2-y2=1的右焦点且与右支有两个交点的直线，其倾斜角范围是（ ）
| A、[0，π） | ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（0，
|
将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD的中点，则AE与平面ABD所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数||z+i|-|z-i||=2对应复平面内的曲线是（ ）
| A、双曲线 | B、双曲线的一支 |
| C、线段 | D、两条射线 |
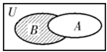已知全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，则图中阴影部分所表示的集合是（ ）| A、{1，2，4} |
| B、{3，7，8} |
| C、{1，2，4，6} |
| D、{3，6，7，8} |