题目内容
不等式（x-5）（6-x）＞6-x的解集是（ ）
| A、（5，+∞） |
| B、（6，+∞） |
| C、∅ |
| D、（-∞，5），（6，+∞） |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：把不等式（x-5）（6-x）＞6-x化为（x-6）2＜0，得出不等式的解集是∅．
解答：
解：不等式（x-5）（6-x）＞6-x可化为
（6-x）（x-5-1）＞0，
即（x-6）2＜0；
∴原不等式的解集是∅．
故选：C．
（6-x）（x-5-1）＞0，
即（x-6）2＜0；
∴原不等式的解集是∅．
故选：C．
点评：本题考查了一元二次不等式的解法问题，对于特殊的一元二次不等式，应根据不等式的特点进行解答，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC的三个内角之比为3：2：1，那么对应的三边之比为（ ）
| A、3：2：1 | ||||
B、
| ||||
C、
| ||||
D、2：
|
已知函数f（x）的定义域为R，若存在常数m＞0，对任意x∈R，有|f（x）|≤m|x|，则称f（x）为F函数．给出下列函数：①f（x）=0； ②f（x）=x2； ③f（x）=sinx+cosx；④f（x）=
； ⑤f（x）是定义在R上的奇函数，且满足对一切实数x1，x2均有|f（x1）-f（x2）|≤2|x1-x2|．其中是F函数的序号是（ ）
| x |
| x2+x+1 |
| A、①②④ | B、①②⑤ |
| C、①③④ | D、①④⑤ |
有四辆不同特警车准备进驻四个编号为1，2，3，4的人群聚集地，其中有一个地方没有特警车的方法共（ ）种．
| A、144 | B、182 |
| C、106 | D、170 |
若k∈R，则k=5是方程
-
=1表示双曲线的（ ）条件．
| x2 |
| k-3 |
| y2 |
| k+3 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
函数f（x）=
x-cosx的零点个数为（ ）
| 1 |
| 8 |
| A、3 | B、4 | C、5 | D、6 |
过双曲线x2-y2=1的右焦点且与右支有两个交点的直线，其倾斜角范围是（ ）
| A、[0，π） | ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（0，
|
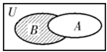已知全集U={x∈N|0＜x≤8}，集合A={1，2，4，5}，B={3，5，7，8}，则图中阴影部分所表示的集合是（ ）| A、{1，2，4} |
| B、{3，7，8} |
| C、{1，2，4，6} |
| D、{3，6，7，8} |