题目内容

1．运行如图所示框图的相应程序，若输入a，b的值分别为log43和log34，则输出M的值是（　　）
A．0B．1C．3D．-1

分析 确定log34＞log43，可得M=log34•log43-2，计算可得结论．

解答 解：∵log34＞1，0＜log43＜1，
∴log34＞log43，
∴M=log34•log43-2=-1，
故选：D．

点评 本题考查程序框图，考查学生的计算能力，属于基础题．

练习册系列答案
相关题目
11．设集合A={x|（x-1）（x-3）＜0}，B={y|y=2x，x∈[1，2]}，则A∩B=（　　）
A．∅B．（1，3）C．[2，3）D．（1，4]
12．一个几何体的三视图如图所示，则该几何体的体积为（　　）
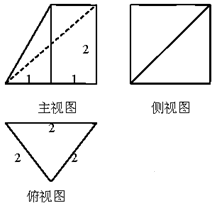
A．2$\sqrt{3}$B．$\sqrt{3}$C．$\frac{{4\sqrt{3}}}{3}$D．$\frac{{2\sqrt{3}}}{3}$
9．设数列{an}的各项都是正数，且对任意n∈N*，都有an2=2Sn-an，其中Sn为数列{an}的前n项和．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=2n+λ•3${\;}^{{a}_{n}}$（n∈N*），若使得对任意n∈N*，都有bn+1＜bn成立，求λ的取值范围．
16．已知函数f（x）=|x+2|-2|x-1|．
（Ⅰ）求不等式f（x）≥-2的解集M；
（Ⅱ）对任意x∈[a，+∞），都有f（x）≤x-a成立，求实数a的取值范围．
6．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点分别为F1（-c，0），F2（c，0），以线段F1F2为直径的圆与双曲线在第二象限的交点为P，若直线PF2与圆E：（x-$\frac{c}{2}$）2+y2=$\frac{{b}^{2}}{16}$相切，则双曲线的渐近线方程是（　　）
A．y=±xB．y=±2xC．y=±$\sqrt{3}$xD．y=±$\sqrt{2}$x
13．已知直线x+2y-1=0与直线2x+my+4=0平行，则m=4．
10．在平面直角坐标系xoy中，直线l：y=2x-4，圆C的半径为1，圆心在直线l上，若圆C上存在点M，且M在圆D：x2+（y+1）2=4上，则圆心C的横坐标a的取值范围是（　　）
A．$[{\frac{3}{5}，2}]$B．$[{0，\frac{12}{5}}]$C．$[{2-\frac{2}{5}\sqrt{5}，2+\frac{2}{5}\sqrt{5}}]$D．$[{0，2-\frac{2}{5}\sqrt{5}}]∪[{2+\frac{2}{5}\sqrt{5}，4}]$
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点为F1，F2，离心率为$\frac{\sqrt{6}}{3}$，点A，B在椭圆上，F1在线段AB上，且△ABF2的周长等于4$\sqrt{3}$．
（1）求椭圆C的标准方程；
（2）过圆O：x2+y2=4上任意一点P作椭圆C的两条切线PM和PN与圆O交于点M，N，求△PMN面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网