题目内容
1．抛物线y=4x2的准线方程为（ ）| A． | x=-1 | B． | x=1 | C． | y=-$\frac{1}{16}$ | D． | y=$\frac{1}{16}$ |
分析 根据题意，将抛物线的方程变形为标准方程，分析可得其焦点位置以及p的值，进而可得其准线方程，即可得答案．
解答 解：根据题意，抛物线y=4x2的标准方程为x2=$\frac{y}{4}$，
其焦点在y轴正半轴上，且p=$\frac{1}{8}$，
则其准线方程为y=-$\frac{1}{16}$；
故选：C．
点评 本题考查抛物线的几何性质，注意将抛物线的方程变形为标准方程．
练习册系列答案
小学课时特训系列答案
相关题目
12．
圆柱被一个平面截去一部分后与长方体组成一个几何体，该几何体的正视图和俯视图如图所示，已知该几何体的表面积为58+12π，则圆柱的半径r=（ ）
圆柱被一个平面截去一部分后与长方体组成一个几何体，该几何体的正视图和俯视图如图所示，已知该几何体的表面积为58+12π，则圆柱的半径r=（ ）| A． | 1 | B． | 2 | C． | $\frac{3}{2}$ | D． | 3 |
9．设随机变量ξ～B（2，p），若P（ξ≥1）=$\frac{5}{9}$，则p的值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{16}{27}$ |
已知函数f（x）=$\sqrt{2}$sin（2x-$\frac{π}{4}$）．
6．一动圆与圆x2+y2=1外切，与圆x2+y2-6x-91=0内切，则动圆的圆心的轨迹是（ ）
| A． | 一个椭圆 | B． | 一条抛物线 | C． | 双曲线的一支 | D． | 一个圆 |
10．在市委市政府扶贫的推动下，安顺某乡镇企业的年产值逐年增长，如表统计了2011～2015年五年的年产值，其中x依次为年份代号（2011年用1代替，其他年份代号顺推），y为年产值（万元）．
参考公式：
回归直线的方程是：$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$．
其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
（Ⅰ）利用最小二乘法计算年产值y（万元）关于年份代号x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅱ）预测2017年该企业的年产值．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 220 | 250 | 285 | 340 | 405 |
回归直线的方程是：$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$．
其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
（Ⅰ）利用最小二乘法计算年产值y（万元）关于年份代号x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅱ）预测2017年该企业的年产值．
13．函数f（x）=2x+ln x2的图象大致为（ ）
| A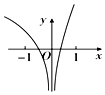． |  | B． |  | C． |  | D． |  |