题目内容
13．函数f（x）=2x+ln x2的图象大致为（ ）| A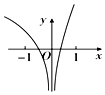． |  | B． |  | C． |  | D． |  |
分析 直接利用特殊值对应点的坐标判断选项即可．
解答 解：当x=-1时，函数f（-1）=2-1+ln（-1）2=$\frac{1}{2}＞0$，对应点的坐标在第二象限，排除B、C、D；
故选：A．
点评 本题考查函数的图象的判断，利用特殊点的位置判断选项是常用方法．
练习册系列答案
春雨教育同步作文系列答案
相关题目
1．抛物线y=4x2的准线方程为（ ）
| A． | x=-1 | B． | x=1 | C． | y=-$\frac{1}{16}$ | D． | y=$\frac{1}{16}$ |
4．以集合U={a，b，c，d}的子集中选出3个不同的子集，需同时满足以下两个条件：（1）U={a，b，c，d}要选出；（2）对选出的任意两个子集A和B，必有A⊆B或B⊆A，那么共有50种不同的选法．
如图，在?ABCD中，∠B=30°，AB=AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F，点M是边AB的一个三等分点，则△AOE与△BMF的面积比为3：4．
5．命题“?x＞0，都有x2-x+3≤0”的否定是（ ）
| A． | ?x＞0，使得x2-x+3≤0 | B． | ?x＞0，使得x2-x+3＞0 | ||
| C． | ?x＞0，都有x2-x+3＞0 | D． | ?x≤0，都有x2-x+3＞0 |
2．设函数f（x）=xex-ax（a∈R，a为常数），e为自然对数的底数．
（1）若函数f（x）的任意一条切线都不与y轴垂直，求a的取值范围；
（2）当a=2时，求使得f（x）+k＞0成立的最小正整数k．
（1）若函数f（x）的任意一条切线都不与y轴垂直，求a的取值范围；
（2）当a=2时，求使得f（x）+k＞0成立的最小正整数k．
3．已知椭圆的标准方程为$\frac{x^2}{5}+\frac{y^2}{4}=1$，F1，F2为椭圆的左右焦点，O为原点，P是椭圆在第一象限的点，则$\frac{{|{P{F_1}}|-|{P{F_2}}|}}{{|{PO}|}}$的取值范围（ ）
| A． | $（{0，\frac{{\sqrt{5}}}{5}}）$ | B． | $（{0，\frac{{2\sqrt{5}}}{5}}）$ | C． | $（{0，\frac{{3\sqrt{5}}}{5}}）$ | D． | $（{0，\frac{{6\sqrt{5}}}{5}}）$ |