题目内容
2．函数f（x）=cos2x的最小正周期为（ ）| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
分析 根据三角函数的周期公式进行计算即可．
解答 解：函数的周期T=$\frac{2π}{2}=π$，
故选：B．
点评 本题主要考查函数的周期的计算，根据三角函数的周期公式是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布N（μ，σ2），下表用茎叶图列举出来抽样出的10名学生的成绩．
7．已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-6x+a，则不等式f（x）＜|x|的解集是（ ）
| A． | （0，7） | B． | （-5，7） | C． | （-5，0） | D． | （-∞，-5）∪（0，7） |
14．某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）．现用分层抽样的方法（按A类、B类分两层）从该工厂的工人中抽取100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数），结果如表．
表1：A类工人生产能力的频数分布表
表2：B类工人生产能力的频数分布表
（1）确定x，y的值；
（2）完成下面2×2列联表，并回答能否在犯错误的概率不超过0.001的前提下认为工人的生产能力与工人的类别有关系？
（3）工厂规定生产零件数在[130，140）的工人为优秀员工，在[140，150）的工人为模范员工，那么在样本的A类工人中的优秀员工和模范员工中任意抽2人进行示范工作演示，试写出所抽的模范员工的人数X的分布列和期望．
下面的临界值表仅供参考：
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
表1：A类工人生产能力的频数分布表
| 生产能力分组 | [110，120） | [120，130） | [130，140） | [140，150） |
| 人数 | 8 | x | 3 | 2 |
| 生产能力分组 | [110，120） | [120，130） | [130，140） | [140，150） |
| 人数 | 6 | y | 27 | 18 |
（2）完成下面2×2列联表，并回答能否在犯错误的概率不超过0.001的前提下认为工人的生产能力与工人的类别有关系？
| 生产能力分组 工人类别 | [110，130） | [130，150） | 总计 |
| A类工人 | 20 | 5 | 25 |
| B类工人 | 30 | 45 | 75 |
| 总计 | 50 | 50 | 100 |
下面的临界值表仅供参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
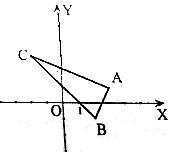己知点A（3，1），点B（2，-1），点C（-2，3）O为原点．则：