题目内容
7．已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-6x+a，则不等式f（x）＜|x|的解集是（ ）| A． | （0，7） | B． | （-5，7） | C． | （-5，0） | D． | （-∞，-5）∪（0，7） |
分析 根据函数奇偶性的性质先求出a的值，以及函数的解析式，进行求解即可．
解答 解：∵函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-6x+a，
∴f（0）=0，即a=0，即当x≥0时，f（x）=x2-6x，
若x＜0，则-x＞0，则f（-x）=x2+6x=-f（x），
即f（x）=-x2-6x，x＜0，
当x≥0时，不等式f（x）＜|x|等价为x2-6x＜x，即x2-7x＜0，即0＜x＜7，
当x＜0时，不等式f（x）＜|x|等价为-x2-6x＜-x，即x2+5x＞0，即x＞0或x＜-5，此时x＜-5，
综上不等式的解为0＜x＜7或x＜-5，
即不等式的解集为（-∞，-5）∪（0，7），
故选：D
点评 本题主要考查不等式的求解，结合函数奇偶性的性质进行转化求解是解决本题的关键．注意要进行分类讨论．
练习册系列答案
相关题目
15．若正数a，b满足ab=a+b+3，则ab的取值范围是（ ）
| A． | （3，9] | B． | [9，+∞） | C． | [9，27] | D． | [27，+∞） |
2．函数f（x）=cos2x的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
12．盒子中有大小形状完全相同的4个红球和3个白球，从中不放回的一次摸出两个球，在第一次摸出的是红球的前提下，第二次也摸出红球的概率为（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
19．
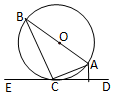如图，AB是圆O的直径，直线CE和圆O相切于点C，AD⊥CE于D，若AD=1，∠ABC=30°，则圆O的面积是（ ）
如图，AB是圆O的直径，直线CE和圆O相切于点C，AD⊥CE于D，若AD=1，∠ABC=30°，则圆O的面积是（ ）| A． | 4π | B． | 6π | C． | 8π | D． | 16π |