题目内容
12.设x,y满足约束条件$\left\{{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}}\right.$,则z=-2x+y的最小值为-5.分析 先根据约束条件画出可行域,再利用几何意义求最值,z=-2x+y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最小值即可.
解答  解:设x,y满足约束条件:$\left\{{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}}\right.$,
解:设x,y满足约束条件:$\left\{{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}}\right.$,
在直角坐标系中画出可行域△ABC,由$\left\{\begin{array}{l}{x+y=1}\\{y=-1}\end{array}\right.$,可得A(2,-1),
所以z=-2x+y的最小值为-5.
故答案为:-5
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20.已知三个函数f(x)=2x+x,g(x)=x-1,h(x)=log3x+x的零点依次为a,b,c,则( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
7.设集合A={-2,-1,0,1,2},B={x|x>-1},则A∩B=( )
| A. | {0,1} | B. | {-1,0} | C. | {-1,0,1} | D. | {0,1,2} |
5.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{1-\frac{x}{2},x<1}\end{array}\right.$,若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1+x2的取值范围是( )
| A. | [4-2ln2,+∞) | B. | [1+$\sqrt{e}$,+∞) | C. | [4-2ln2,1+$\sqrt{e}$) | D. | (-∞,1+$\sqrt{e}$) |
2.函数f(x)=cos2x的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
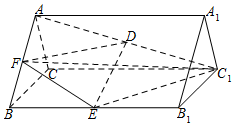 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点. 已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.
已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.