题目内容
若方程x2-2mx+4=0的两根满足一根大于2,一根小于2,则m的取值范围是( )
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,+∞) |
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:令f(x)=x2-2mx+4,由题意可得f(2)<0,从而求得m的范围.
解答:
解:令f(x)=x2-2mx+4,由方程x2-2mx+4=0的两根满足一根大于2,一根小于2,
可得f(2)=8-4m<0,求得 m>2,
故选:B.
可得f(2)=8-4m<0,求得 m>2,
故选:B.
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( )
A、3
| ||||
B、(5+3
| ||||
C、
| ||||
D、
|
直线x-y=0被圆x2+y2=1截得的弦长为( )
| A、2 | B、1 | C、4 | D、3 |
设x=lnπ,y=log
,z=e-
,则( )
| 5 |
| 2 |
| 1 |
| 2 |
| A、y<z<x |
| B、z<x<y |
| C、z<y<x |
| D、x<y<z |
已知两个变量x,y具有线性相关关系,并测得(x,y)的四组值分别是(2,3)、(5,7)、(8,9)、(11,13),则求得的线性回归方程所确定的直线必定经过点( )
| A、(2,3) |
| B、(8,9) |
| C、(6,9) |
| D、(6.5,8) |
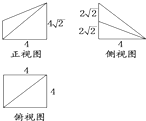 如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为
如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为