题目内容
已知函数f(x)=
(x∈(-1,1)),有下列结论:
(1)?x∈(-1,1),等式f(-x)+f(x)=0恒成立;
(2)?m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
(3)?x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2);
(4)存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为 .
| x |
| 1-|x| |
(1)?x∈(-1,1),等式f(-x)+f(x)=0恒成立;
(2)?m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
(3)?x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2);
(4)存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为
考点:命题的真假判断与应用,函数的值
专题:函数的性质及应用,简易逻辑
分析:(1)根据函数奇偶性的定义判断函数是奇函数即可.
(2)判断函数|f(x)|的奇偶性和最值即可判断.
(3)根据分式函数的性质判断函数的单调性.
(4)根据函数图象以及函数奇偶性的性质进行判断.
(2)判断函数|f(x)|的奇偶性和最值即可判断.
(3)根据分式函数的性质判断函数的单调性.
(4)根据函数图象以及函数奇偶性的性质进行判断.
解答:
 解:(1)∵f(x)=
解:(1)∵f(x)=
,x∈(-1,1),
∴f(-x)=
=-
=-f(x),x∈(-1,1),
即函数f(x)为奇函数,
∴f(-x)+f(x)=0恒成立.∴(1)正确
(2)∵f(x)=
,x∈(-1,1)为奇函数,
∴|f(x)|为偶函数,
当x=0时,|f(0)|=0,
∴当m=0时,方程|f(x)|=m只有一个实根,当m>0时,方程有两个不等实根,∴(2)错误.
(3)当x∈[0,1)时,f(x)=
=
≥0,为增函数.
当x∈(-1,0]时,f(x)=
=
≤0,为增函数.
综上函数f(x)在(-1,1)上为单调函数,且单调递增,
∴?x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2)成立,即(3)正确.
(4)由g(x)=f(x)-kx=0得f(x)=kx,
∴f(0)=0,即x=0是函数的一个零点,
又∵函数f(x)为奇函数,且在(-1,1)上单调递减,
∴可以存在无数个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有3个零点,如图:
∴(4)正确.
故(1),(3),(4)正确.
故答案为:(1),(3),(4)
 解:(1)∵f(x)=
解:(1)∵f(x)=| x |
| 1-|x| |
∴f(-x)=
| -x |
| 1-|-x| |
| x |
| 1-|x| |
即函数f(x)为奇函数,
∴f(-x)+f(x)=0恒成立.∴(1)正确
(2)∵f(x)=
| x |
| 1-|x| |
∴|f(x)|为偶函数,
当x=0时,|f(0)|=0,
∴当m=0时,方程|f(x)|=m只有一个实根,当m>0时,方程有两个不等实根,∴(2)错误.
(3)当x∈[0,1)时,f(x)=
| x |
| 1-|x| |
| x |
| 1-x |
当x∈(-1,0]时,f(x)=
| x |
| 1-|x| |
| x |
| 1+x |
综上函数f(x)在(-1,1)上为单调函数,且单调递增,
∴?x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2)成立,即(3)正确.
(4)由g(x)=f(x)-kx=0得f(x)=kx,
∴f(0)=0,即x=0是函数的一个零点,
又∵函数f(x)为奇函数,且在(-1,1)上单调递减,
∴可以存在无数个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有3个零点,如图:
∴(4)正确.
故(1),(3),(4)正确.
故答案为:(1),(3),(4)
点评:本题主要考查分式函数的性质,利用函数奇偶性,单调性以及数形结合是解决本题的关键,综合性强,难度较大,本题的质量较高.

练习册系列答案
相关题目
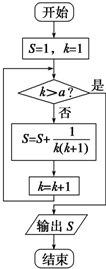
某程序框图如图所示,若该程序运行后输出的值是
,则a的可能值为( )
| 9 |
| 5 |

| A、4 | B、5 | C、6 | D、7 |
在R上定义运算?:x?y=x(1-y)若对任意x>2,不等式(x-a)?x≤a-2都成立,则实数a的取值范围是( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、(3,+∞) |
| D、[3,+∞) |